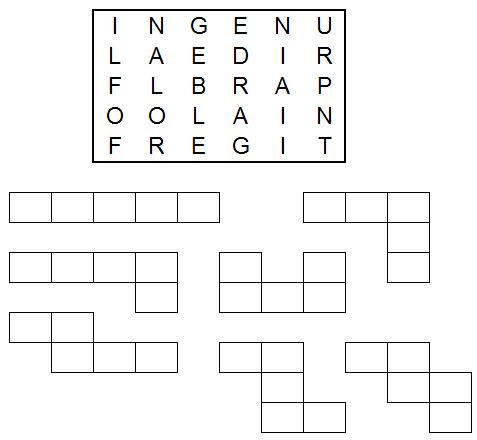
The object of this game is to try to score as highly as possible by using letters in a given rack to form words. Just like in real ten pin bowling, you have a maximum of two attempts at each rack.
If you get a ten-letter word, that is a Strike and is worth 20 points.
If you find two words that between them use each of the ten pins once each, that is a Spare and is worth 15 points.
Any fewer than that, just total up the letters used to give your point total. So if you find a five-letter word and a three-letter word, that rack will have scored you 8 points.
I have randomly generated the racks by drawing 50 scrabble tiles out, discarding only the blanks (unlike the previous outing of this puzzle, where I tweaked it so that at least a spare was achievable on each rack - this way I can legitimately take part myself).
What is the highest total you can achieve over the five racks?