Your Custom Text Here
Asking for the probability was a deliberate red herring, since it’s actually impossible for the last pebble to be white.
The only way of removing black pebbles is if both selected pebbles are black, at which point they are both discarded. But since we start with an odd number of black pebbles, we will still have an odd number of black pebbles throughout the game. Therefore the final pebble will be black. The probability the last pebble is white is 0.
If we scale up the figure by the square of the hypotenuse of the 5,12,13 triangles, (namely 169), then the fourth triangle will have sides of 828,2035,2197 and since these numbers have a GCD of 1, that is the primitive form of the Pythagorean triangle we were seeking.
There are two possible arrangements where all the lengths are integers, but in both the red line is 2304 long.
The height is at a minimum when the four triangles are similar, and so therefore the bottom right corner will be four equal angles of 22.5 degrees. The length of the first hypotenuse will be sec(22.5), and the second will be the square of that, etc. The height of the rectangle will be the fourth power of sec(22.5) which is equal to 24-16*sqrt(2), which is approximately equal to 1.3726.
We are given:
1/a = 1+b
1/b = 3+c
1/c = 4+b
If we invert the third equation we have an expression for c that we can use in the second equation.
c=1/(4+b)
1/b = 3+1/(4+b)
1/b = (3(4+b)+1)/(4+b) = (13+3b)/(4+b)
Cross multiplying we get a quadratic:
3b^2+12b-4 = 0
The value of b that lies between 0 and 1 is (4*sqrt(3)-6)/3
We can put this into the first equation:
1/a = 1+(4*sqrt(3)-6)/3 = (3+4*sqrt(3)-6)/3 = (4*sqrt(3)-3)/3
a = 3/(4*sqrt(3)-3), which does fulfil the requirements of the question, but we’d prefer to not have irrationals in the square root:
a = 3/(4*sqrt(3)-3)*(4*sqrt(3)+3)/(4*sqrt(3)+3)=
(12*sqrt(3)+9)/(48-9) = (4*sqrt(3)+3)/13
Since, if we find a valid figure we can scale it by ‘h’ in the horizontal and ‘1/h’ in the vertical to find any one of an infinite family of solutions, we can, without loss of generality, specify the particular figure where A = C. And since that top triangle of area 8 is similar to the figure as a whole we can also say that B = C+D+E.
A and C must both be equal to 4 to form the triangle of area 8. To form the triangle of area 4, D must equal 2.
From the triangle of area 20, B*E must be 40.
We know that B = C+D+E, and we also know the values of C and D, therefore E = B-6. So B*(B-6)=40. We could solve this as a quadratic, or else we can just look for two positive numbers 6 apart whose product is 40, namely 10 and 4.
So if B = 10, the entire figure has area 50, and if we subtract the known areas we find that area x = 7.
PS: If I wanted to be a little more general I would just multiply all of the horizontal lengths in the above solution by h and all the vertical distances by 1/h and when calculating the areas all hs would cancel.
I’m going to make use of a theorem called Ceva’s Sine theorem, which states that, in the below figure, the product of the sines of angles a, c and e is equal to the product of the sines of angles b, d and f.
In our question, a and d are unknown, and b, c, e and f are 6, 24, 12 and 54 respectively.
sin(a).sin(24).sin(12) = sin(6).sin(d).sin(54)
(sin(24).sin(12))/( sin(6).sin(54)) = sin(d)/sin(a)
sin(d)/sin(a) = 1
sin(d) = sin(a)
But since the six angles must total 180 degrees, a + d = 84, therefore a = d = 42.
So our unknown angle x is equal to 42 degrees.
The merged lane will need to have twice as many cars passing a given point in a given time period than the initial pair of lanes, or conversely will take half the time for each car to pass a given point.
Say the initial speed is x (mph), then the stopping distance is (x^2)/20 + x/2 (ft).
If we take this distance and divide by the speed x we will know the time taken for each car to pass a given point. (The units for this are 15/22 seconds, but we don’t need to worry about that since it’s the same whatever the speed).
The formula for this measure is x/20 + 1/2.
To merge the lanes we need to find a value y such that y/20 + 1/2 is half as much as x/20 + 1/2:
y/10 + 1 = x/20 + 1/2
y/10 = x/20 – 1/2
y = x/2 – 5
For our puzzle x=60, and so therefore y = 25mph.
The maximum is 81643572, 27+16+7+12=62
The minimum is 27163548, 9+4+7+8=28
Since both 8 and 4 are powers of 2, we can rewrite them as 2^3 and 2^2 respectively:
2^(3(x-1)) = 2^(2(x+2))
2^(3x-3) = 2^(2x+4)
3x-3 = 2x+4
x = 7
3x-3 = 2x+4 = 18
2^18 = 262144
N is equal to 262144.
It turns out that the largest semicircle, the one with unit radius, sits in the middle of the segment.
The circle radius is 2, and the segment has an angle to the centre of the circle of 120 degrees.
You might notice that each pair of adjacent terms has a GCD greater than 1, for instance 21 and 119 are both divisible by 7, and 697 and 4059 are both divisible by 41. In fact on further inspection, each term appears to be the product of adjacent terms of a second sequence: 1,3,7,17,41,99,etc. It looks as if the definition of this second sequence (after the initial two terms) is that each term is twice the previous term, plus the term before that. If that is confirmed to be the case, the only way a term in the product sequence can be prime is if one of the two factors is 1 (and the other is itself prime). This is only the case for the term ‘3’, and so therefore this is the only prime number that will appear in the entire infinite sequence.
But how do we prove that the given sequence is the products of adjacent terms of the second sequence?
That is equivalent to proving the claim that if a=2b+c, b=2c+d and c=2d+e then it follows that ab=5bc+5cd-de.
Let’s start with the product relation but substitute a=2b+c
(2b+c)b=5bc+5cd-de
2bb+bc=5bc+5cd-de
2bb=4bc+5cd-de
Next replace any instances of b with 2c+d
2(2c+d)(2c+d)=4(2c+d)c+5cd-de
8cc+8cd+2dd=8cc+4cd+5cd-de
2dd=cd-de
Finally replace c with 2d+e
2dd=(2d+e)d-de
2dd=2dd+de-de
Since both sides are evidently equal, that proves that the three relations are equivalent to the product relation.
First let’s figure out the radius of the semicircles. Lines from the ends of the chord to the centre of the circle will bisect the angles of the equilateral triangles, forming 30 degrees angles. From this we can work out that the perpendicular distance from the centre of the unit circle to the chord is 1/2.
We can now set up a Pythagorean triangle with the radius R of the semicircles as an unknown.
(1-R)^2 = R^2 + 1/4
1 - 2R + R^2 = R^2 + 1/4
1 - 2R = 1/4
3/4 = 2R
R = 3/8
If the distance from the centre to the chord is 1/2, then so too is the distance from the chord to the top of the circle. Again we can set up a Pythagorean triangle, this time with the radius of the small circle as the unknown:
(3/8+r)^2 = (3/8)^2 + (1/2-r)^2
(3/8)^2 + 3r/4 + r^2 = (3/8)^2 + 1/4 – r +r^2
3r/4 = 1/4 - r
7r/4 = 1/4
r = 1/7
If the letters of the alphabet were put in rows of three then each set of words can be made from only the letters in a given column.
A B C
D E F
G H I
J K L
M N O
P Q R
S T U
V W X
Y Z
Trying the same thing with two columns is a problem since all of the vowels A, E, I, O and U, and even the occasional vowels Y and W will all appear in the left hand column, and the right hand column would be reduced to onomatopoeic non-words like BZZZ and PFFT.
The first thing to do is to establish the size of the square. If we assume that the L-triomino is made up of three unit squares, the diameter of the circle will be the hypotenuse of a triangle with base 5 units and height 3 units.
This diameter, and therefore also the side length of the square, is the square root of 34.
If we place an L-triomino in each corner, then tilt the square 45 degrees, how large a square can we fit in the remaining space?
The side of the whole square is sqrt(34), so the diagonal is sqrt(68). From this we need to take off twice the diagonal of a 1.5 x 1.5 square to find the side length of the inner square.
These combine to be sqrt(18). So sqrt(68)-sqrt(18) = 4.0036…
Just to be safe we need to confirm that the diagonal of the inner square doesn’t exceed the side length of the larger square, or else the corners will extend beyond the original square. This isn’t the case so we are safe to continue.
How many L-triominoes can we fit in this 4x4 square? If we place one in each corner we have space for a fifth in the middle. Added to the four we already placed means that overall we can fit 9 L-triominoes in the square of area 34 square units.
Of course this doesn’t prove that 10 or 11 isn’t possible (more than 11 is impossible as the area of the triominoes would be greater than that of the square), but such a proof is a little more involved.
21978 x 4 = 87912
If we assume that the red squares measure 1x1, then the red region has an area of 10 square units.
The next step is to establish the dimensions of the blue square.
The top left and bottom left triangles in the above figure are similar, so (2+x)/1 = 2/x. Cross-multiplying and solving the resulting quadratic we find that x = sqrt3-1, or about 0.732.
Using Pythagoras the side length of the blue square is therefore sqrt(8+2sqrt3), and the area of the full square is 8+2sqrt3.
From that we have to subtract the two triangles A and B. A has height 1 and base x. B has base 1+x and is similar to A. From this we find that A has an area of (sqrt3-1)/2 and B has an area of 3(sqrt3-1)/2.
This means that the visible blue region is also 10 square units.
The horizontal component of the lower right side of the blue square is the same as the vertical component of the lower left side, so 2 units, so the overall rectangle has sides 5 and 6. Therefore the green region also has area of 10 square units.
The areas of the red, blue and green regions are all identical.
If you scale the entire figure by x in the horizontal direction and 1/x in the vertical dimension all of the areas will be preserved. By setting x to the fourth root of 3 (approximately 1.316) the equilateral triangles are all transformed into right-angled isosceles triangles with height half of their bases, so that a triangle with area n^2 will have height n and base 2n. Now it is simple to find the area of the trapezoid of base 19, and then subtract the triangles and half triangles to find the required area.
The trapezoid has area 19x7/2, from which we must subtract 16/2, 9, 1, 4 and 9/2.
The answer is therefore 40 square units.
Opposite sides of a rhombus are parallel and the same length, therefore the length and orientation of the lower left side of the square are identical to the right hand slope of the triangle with base 18. Similarly the lower right side of the square has the same length and orientation as the left slope of the 38 base triangle. We can now dispense with the rest of the diagram and only look at those two triangles, armed with the knowledge that the angle between them is 90 degrees. This also means that the length of the other two triangle bases was irrelevant, so long as they produced valid triangles.
Dropping perpendicular bisectors from each we get two congruent right angled triangle with legs 9 and 19.
Since the area we seek is simply x^2, we can use Pythagoras to find that the area of the original square is 9^2+19^2, which is equal to 442.
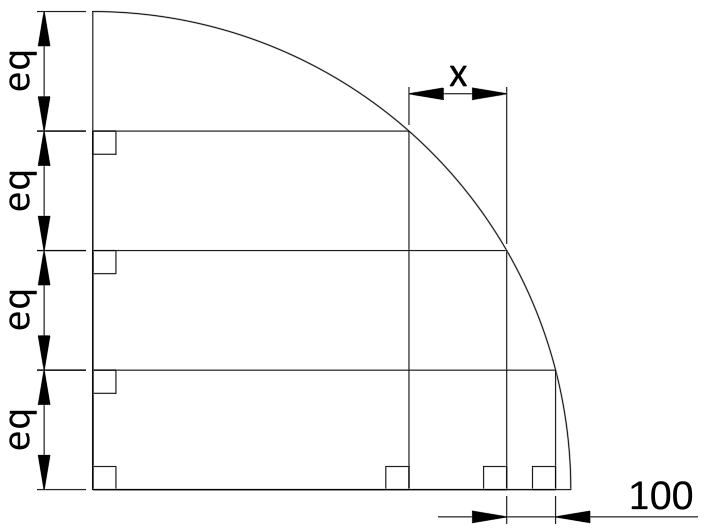
Let’s call the equal heights h. The radius of the quarter circle and therefore also the diagonal of each of the three main rectangles is 4h. The horizontal length of each of those rectangles, let’s call them k,l,m can be found using Pythagoras:
k^2=(4h)2-h^2=15h^2
l^2=(4h)2-(2h)^2=12h^2
m^2=(4h)2-(3h)^2=7h^2
k=h*sqrt(15)
l=h*sqrt(12)
m=h*sqrt(7)
Now 100 and x are simply the difference between those lengths:
100=k-l=h*(sqrt(15)-sqrt(12))
x=l-m=h*(sqrt(12)-sqrt(7))
If we divide one equation by the other we can eliminate h:
x/100 = (sqrt(12)-sqrt(7))/(sqrt(15)-sqrt(12))
x/100 = 2.0014
x = 200.14, or 200 to the nearest integer.
Why should (sqrt(12)-sqrt(7))/(sqrt(15)-sqrt(12)) be so close to 2?
None of 7 12 or 15 is a square number so we can’t reduce them any further. When we factorise them nothing useful happens. However if we multiply each of them by 24, the above ratio will be preserved, and although 168, 288 and 360 still aren’t square numbers, the numbers just above them, 169, 289 and 361 all are (squares of 13, 17 and 19 respectively).
The value of (sqrt(289)-sqrt(169))/(sqrt(361)-sqrt(289)) is precisely 2, so it should come as no surprise that (sqrt(288)-sqrt(168))/(sqrt(360)-sqrt(288)) is so close to 2, and THAT ratio is precisely the same as the one in the question.
Why is it that when we multiply each of the numbers (7,12,15) by 24 we get a number one less than a square? Is that just a coincidence? Is it always possible so multiply a set of numbers by a particular factor so that the products are all one less than a square? These are interesting questions.