I have a polyhedron with the properties that every vertex is at the junction of exactly three faces, two of its faces are heptagons, and all its other faces are pentagonal.
How many pentagonal faces are there?
Puzzle of the Week #240 - Base 4 Code
I have written a sentence, and I have replaced each of the letters with the numbers that denote their position in the alphabet. However, I have used the base 4 number system.
Be careful, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10).
1103 11311 11311 11311 12213210 11311 110211 3233110 3211110230121 1103 1132110311 1103 11311 20331001110 11033 2113333111.
Puzzle of the Week #239 - Nearly Equal Corners
A rectangle is split into four triangles as below. The areas of the three corner pieces are almost equal, with one being just 1 square unit larger than the other two. The remaining area is 1597 square units. What is the value of x?
Puzzle of the Week #238 - Circle Box
Here’s a fun challenge. The task is to fit circles into a grid according to the following rules:
· The centre of every circle must lie on a lattice-point of the grid, and no circles can share the same centre point.
· Every circle must have a whole number as its radius.
· The circles can touch each other and the edge of the grid, but cannot cross. In other words a circle can be entirely inside another, or entirely outside, but not partially inside.
· Your ‘score’ is the total area of all the circles you can fit in. A radius-1 circle has area of 1(pi), a radius-2 circle has an area of 4(pi), radius-3 = 9(pi), etc.
· The example 4 x 4 unit grid has a score of 6(pi) (4+1+1). I have marked the centre of each circle to show that none coincide.
What score can you achieve in the 12 x 12 unit grid?
Puzzle of the Week #237 - Right Angled Triangle Spiral
I have begun to construct a spiral of right-angles triangles thus:
The first triangle has legs both equal to 1.
Each subsequent triangle uses the hypotenuse of the previous triangle as one leg and a new line of length 1 as the other leg.
Every time the length of a spoke happens to be an exact whole number, I’ve marked it in red. I happened to notice that the angular distances between the red spokes are of a similar size.
My question is this: is it converging, and if so, to what?
Puzzle of the Week #236 - Zigzag
A zigzag of lines is drawn in a circle. The combined length of the three horizontal lines is exactly equal to the combined length of the two diagonal (parallel) lines. What is the angle formed between the horizontal and diagonal lines?
Puzzle of the Week #235 - Shaded Area
Puzzle of the Week #234 - Split Squad
A junior football team has 15 players, with squad numbers from 1 to 15.
During training they split into two teams: a team of 7 and a team of 8, such that:
The sum of the squad numbers on team A is the same as the sum of the squad numbers on team B.
The sum of the squares of the squad numbers on team A is the same as the sum of the squares of the squad numbers on team B.
The sum of the cubes of the squad numbers on team A is the same as the sum of the cubes of the squad numbers on team B.
How was the squad split into the two teams?
Puzzle of the Week #233 - Simple but Complex
If x + y = 4, and x^2 + y^2 = 6, what are the values of x and y?
Puzzle of the Week #232 - Five Towns
There are five towns: Anderton, Barmby, Calderwood, Dempsey and Edinburgh.
There are straight roads between Anderton, Barmby and Calderwood.
Dempsey is exactly 25 miles from Anderton, Barmby and Calderwood.
Edinburgh is exactly 12 miles to the closest point on each of the roads between Anderton, Barmby and Calderwood.
How far is Dempsey from Edinburgh?
Puzzle of the Week #231 - Mastermind
You may be familiar with the game ‘Mastermind’, where one player forms a code of coloured pegs and another makes guesses. The coder tells the guesser after each guess how many pegs are fully correct, and how many others are present but in the wrong place.
My version is different from the standard version in three respects:
a) Instead of four, the code is now FIVE pegs long.
b) Instead of six different colours to choose from, in this version there are only TWO different colours of pegs: RED and YELLOW. There are therefore 2 to the power of 5, (32), different possible codes the coder might have set.
c) The guesser has decide what their first ‘n-1’ guesses are going to be straight away, before getting any feedback from the coder, such that when the feedback ultimately comes, the guesser can be certain of guessing correctly on the very next guess, the ‘nth’ guess (or earlier if one of the original n-1 guesses happened to have been correct). (In other words, if the guesser decides on 9 guesses and knows that whatever the code happens to be, they can use the feedback from those 9 guesses to be certain that the 10th guess will be correct, then n equals 10).
The question is then: what is the minimum value of ‘n’, such that the nth guess is guaranteed to be correct?
Puzzle of the Week #230 - Cairo-Word
I have taken a section of a Cairo tiling pattern and populated it with four-letter-words. To be helpful to you in your task of reconstructing it, I’ve given you both the list of words and the staring position and the direction of each of the words in the grid.
Puzzle of the Week #229 - Perfect Power Pairs
Most numbers cannot be expressed as a^b + c^d, where a and c are prime numbers and b and d are integers greater than 1. However there is one set of 6 consecutive numbers that all can, what are they?
Puzzle of the Week #228 - Ellipse
Below is a portion of an ellipse. The semi-minor axis has length 5. A 45 degree diagonal line from the centre to the edge of the ellipse has length 7.
What is the length of the semi-major axis?
If it helps, the general equation for an ellipse is:
(x/a)^2 + (y/b)^2 = 1, where a and b are the two semi-axes.
Puzzle of the Week #227 - Scrabble Ten-Pin Bowling
Here’s something a little different for you this week. This is a game I invented which you can play on your own or against others. All you need is a bag of tiles from a standard Scrabble set. Randomly draw out ten tiles and arrange them in a triangle. This is the first frame of the game of ten-pin bowling. If you can form a ten-letter word, you have scored a strike. If you can form two words using each of the ten letters exactly once each, this is a spare. If you can do neither, try to use as many letters as possible in at most two words. Scoring is exactly the same as for ten-pin bowling. Continue for all ten frames (there are 100 letters in a scrabble set), and then tot up your score.
If you’re not familiar with the scoring system of ten-pin bowling I’ll briefly explain: you get points for each word, equal to how many letters in the word. In addition, if you get a spare (use all letters in one frame using two words), you get bonus points equal to the next word you score.
If you get a strike (a ten letter word), you get bonus points equal to the next two words you score.
If you only get one word in a frame, and it's not a strike, then for the purposes of bonus points, you get a zero length word too.
In real tenpin bowling, if you get a strike or a spare on the tenth frame, you get an eleventh frame to determine your bonus points, and if you were lucky enough to get a strike on the tenth and eleventh frames, you would get a twelfth frame.
In this game, there are no eleventh and twelfth frame, so to determine any bonus points you are entitled to after the tenth frame, look back at the words you scored in the first and second frames.
So that’s the general outline of the game. For the purposes of this Puzzle of the Week I’ve randomly generated a complete game. Try to resist using solving tools as it takes the fun out of it, and see what the highest score you can achieve by only spending a minute on each frame.
For reference I scored a modest 95 points. But then this is a particularly tough board! I don’t believe there are any strikes up for grabs (prove me wrong!), but a spare is possible on at least some of the frames.
Puzzle of the Week #226 - Crazy Currency
In Elbonia they only have three denominations of coins: 15 ELB, 21 ELB and 35 ELB. Although each pair of these coins have a common factor, all three do not. This means that if the value is high enough, any value can be expressed exactly with no change required. But what is the highest amount that cannot be expressed exactly?
Puzzle of the Week #225 - Six Integers
x^2 = a^2 + 4b + 1
y^2 = b^2 + 4c + 1
z^2 = c^2 + 4a + 1
a, b, c, x, y, z are all positive integers
a > b > c
x > y > z
What are the values of the six integers?
(There is a really neat algebraic trick you can use here. First see if you can calculate x in terms of a).
Puzzle of the Week #224 - How Many Coins
I have a number of coins. I throw them all, count how many heads and how many tails and multiply those two numbers together. I calculate what the expected (average) answer should be and discover it is exactly three times the number of coins. How many coins do I have?
(For instance if there were three coins, there are eight possibilities:
HHH TTT HHT HTH THH TTH THT HTT
The first two result in 3 x 0 = 0, and the other six result in 2 x 1 = 2, so the average answer is 1.5)
Puzzle of the Week #223 - Winston Churchill
I have a six letter word, a clue to which is: ‘Something Winston Churchill often is’.
If I change the first letter of my word to the letter that follows it in the alphabet, and then reverse the entire word, I get a new word.
What was my word?
Puzzle of the Week #222 - Staircase Rings
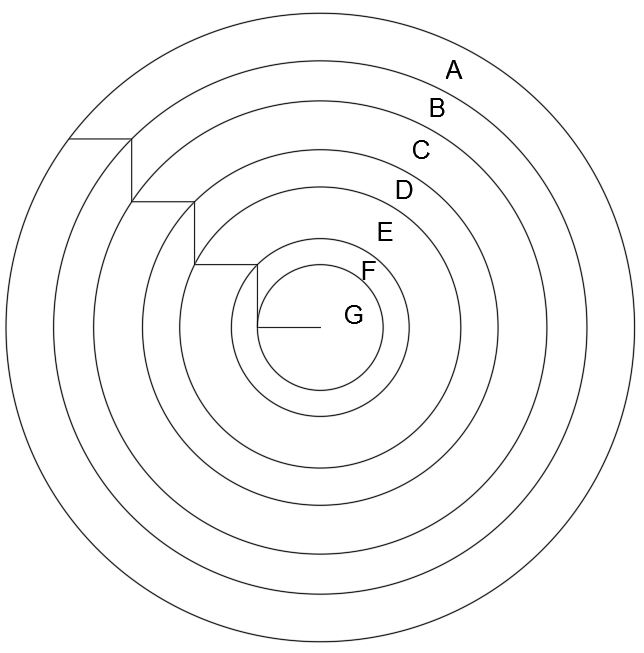
In the following diagram, the ‘staircase’ is made up of horizontal and vertical lines of equal length. The ends of these lines determine the radius of each of the rings, whose shared centre is the end of the final horizontal line.
If the overall shape has an area of 100, what is the area of each of the individual regions A to G?
