Can you work out what the total angle is at the top of this triangle, without using a calculator?
Puzzle of the Week #263 - 24-gon
Puzzle of the Week #262 - Hexagon Area
Inside a regular hexagon lines are drawn from four of the corners to a point inside as shown. The three triangles that result have areas of 3, 5 and 9 respectively. What is the area of the entire hexagon?
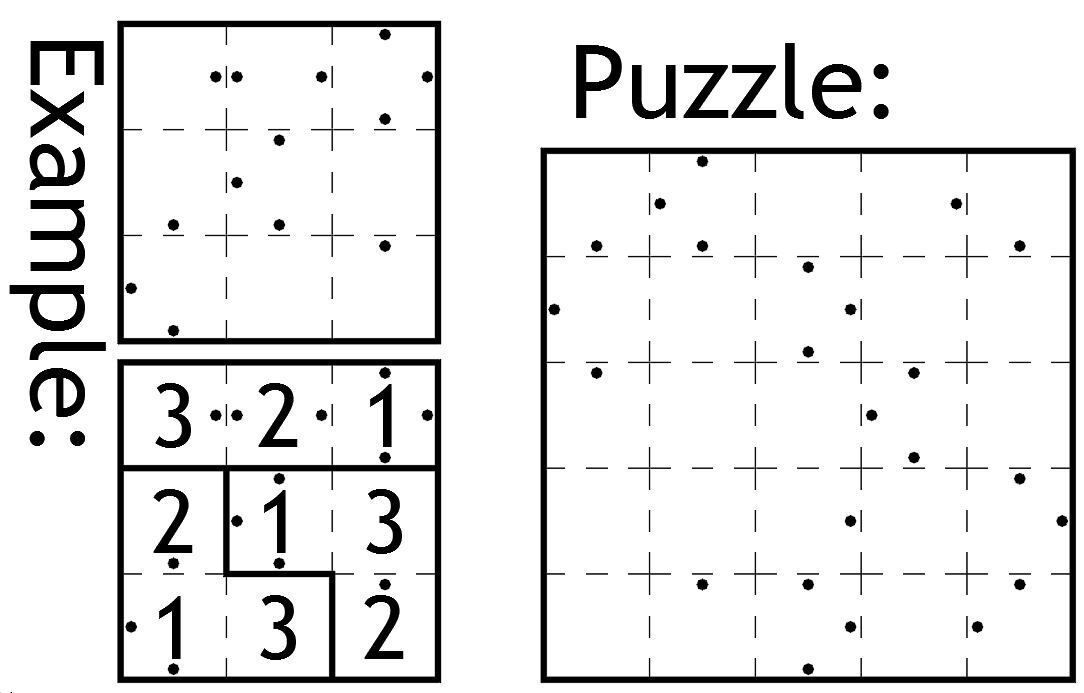
Puzzle of the Week #261 - Su-Dot-U
Your task is to solve this irregular sudoku (the digits 1 to 5 appearing once each in every row, column and 'shape').
Except that I haven't told you where the boundaries between the shapes are; instead I've placed dots in any square where the number to be placed in the square denotes how many squares (including the one with the dot in) until you get to the next boundary line in the direction of the dot.
Clear as mud? Hopefully the attached example 3x3 will help. For instance, the 2 in the middle of the top row, combined with the left and right dots, says that in each direction left and right from that square there are two squares (including the one with the 2 and the dots in) before you get to a boundary line (which happens to be the outer boundary of the entire grid).
In both the example and the puzzle, I have placed dots in every position that I could, according to the rules.
A hint to get you started: if a dot appears next to the outside boundary of the grid, then that square must contain a 1.
Puzzle of the Week #260 - Semi-grams
Rearrange the letters in each of these ten five-letter words and then pair them up to form five ten-letter words. I’ve completed one of the ten letter words to start you off:
First halves:
(ALERT) METRO NOTED TIMES UPSET
Second halves:
GIANT (RATIO) ROAST SENSE SOUND
Example solution:
ALERT + RATIO = RETAL + IATOR = RETALIATOR
Puzzle of the Week #259 - Triangle Area (Tough)
I have to warn you, this puzzle is tougher that the ones I would ordinarily be prepared to publish. However, be reassured that it can be solved just using high school maths. Aficionados of my puzzles will know that wherever I can I engineer the puzzle so that the solution is a whole number. This puzzle is no exception in that regard. Good luck!
Puzzle of the Week #258 - Su-Dot-U
Back by popular demand!
Your task is to solve this irregular sudoku (the digits 1 to 6 appearing once each in every row, column and 'shape').
Except that I haven't told you where the boundaries between the shapes are; instead I've placed dots in any square where the number to be placed in the square denotes how many squares (including the one with the dot in) until you get to the next boundary line in the direction of the dot.
Clear as mud? Hopefully the attached example 3x3 will help. For instance, the 2 in the middle of the top row, combined with the left and right dots, says that in each direction left and right from that square there are two squares (including the one with the 2 and the dots in) before you get to a boundary line (which happens to be the outer boundary of the entire grid).
In both the example and the puzzle, I have placed dots in every position that I could, according to the rules.
A hint to get you started: if a dot appears next to the outside boundary of the grid, then that square must contain a 1.
Puzzle of the Week #257 - Two Squares
Two squares are arranged as shown, one of them rotated 45 degrees with respect to the other, and the perimeters of the two squares coinciding at three points.
What is the ratio of the areas of the two squares?
Puzzle of the Week #256 - Su-Dot-U
Your task is to solve this irregular sudoku (the digits 1 to 5 appearing once each in every row, column and 'shape').
Except that I haven't told you where the boundaries between the shapes are; instead I've placed dots in any square where the number to be placed in the square denotes how many squares (including the one with the dot in) until you get to the next boundary line in the direction of the dot.
Clear as mud? Hopefully the attached example 3x3 will help. For instance, the 2 in the middle of the top row, combined with the left and right dots, says that in each direction left and right from that square there are two squares (including the one with the 2 and the dots in) before you get to a boundary line (which happens to be the outer boundary of the entire grid).
In both the example and the puzzle, I have placed dots in every position that I could, according to the rules.
A hint to get you started: if a dot appears next to the outside boundary of the grid, then that square must contain a 1.
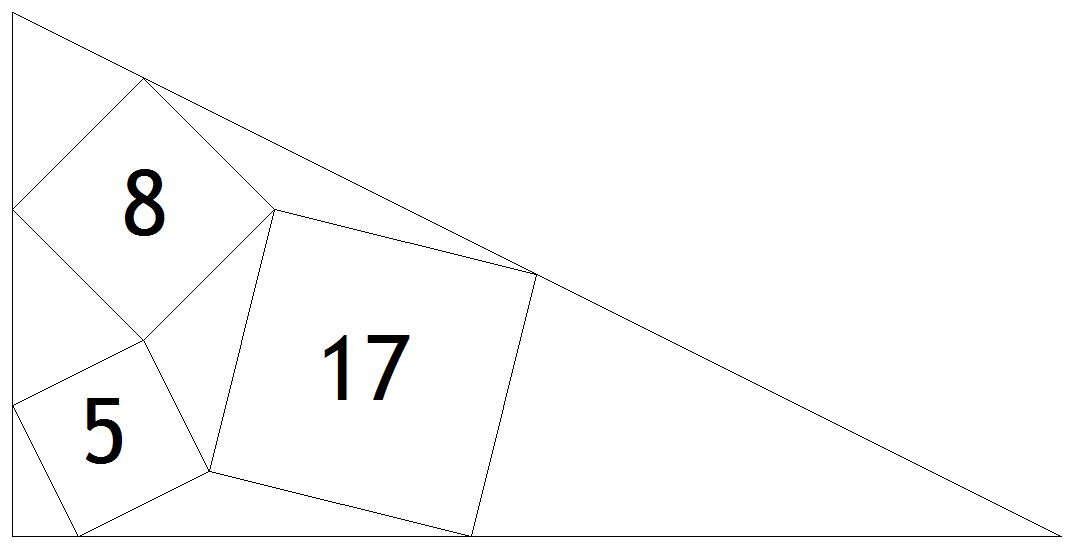
Puzzle of the Week #255 - Three Squares in a Triangle
Three squares of area 5, 8 and 17 respectively, fit within a triangle as shown.
What is the area of the overall triangle?
Puzzle of the Week #254 - Three Squares in a Hexagon
Three squares fit in a hexagon as shown. The areas of the three squares are 200, 162 and 578 respectively.
What is the area of the entire hexagon?
Puzzle of the Week #253 - Build-a-Crossword
I have taken a completed crossword grid, removed all the consonants to the end of the row and/or column that they belong in, and then changed all the black squares into random vowels.
Your task is to reconstruct the crossword by figuring out which of the vowels are genuine and which need to become black squares, and by putting the consonants all back into place. Good luck!
Puzzle of the Week #252 - Hexagon Angle
Take a regular hexagon ABCDEF as below. Draw a line from A to a point midway between B and C, and another line from A to a point midway between D and F.
What is the angle between those two lines?
Puzzle of the Week #251 - Trispace
I have an equilateral triangle, dissected into three trapezoids and a smaller equilateral triangle. The PERIMETERS of the three trapezoids are 52, 66 and 80 respectively. The side length of the overall equilateral triangle (a) is precisely 13 times the side length of the smaller equilateral triangle (b).
What is the value of a?
Puzzle of the Week #250 - Squarespace
Four rectangles with areas as shown can be arranged to form a SQUARE with a SQUARE space left in the middle.
What is the area of the square space?
Puzzle of the Week #249 - Tetrahedron Packing
You have a tetrahedron-shaped space with a side length of 5 along each edge.
How many solid tetrahedrons of side length 1 can you fit into the space?
Puzzle of the Week #248 - Quartet
The four numbers 2,3,4 and 8 can be combined in pairs in six different ways, and the product of those six pairs will be
2 x 3 = 6
2 x 4 = 8
3 x 4 = 12
2 x 8 = 16
3 x 8 = 24
4 x 8 = 32
The sum of the original four numbers (2, 3, 4 and 8) is 17.
Can you find a different quartet of POSITIVE numbers whose products of pairs are also 6, 8, 12, 16, 24 and 32, but whose sum is less than 17?
Puzzle of the Week #247 - Diophantine Parallelogram
All of the lines on this diagram are integer lengths.
DE = 13
AD = BD
AB is parallel to CE
AC is parallel to BE
Angle CAD = angle DAB
What is the length of AD?
Puzzle of the Week #246 - Ghost Crossword
Use logic to fill in the crossword grid given only the clue numbers and the following rules:
1) The crossword is numbered in the usual way.
2) The grid is fully symmetrical.
3) The white area must all be connected together.
4) ‘Words’ are at least three letters long.
5) No 2x2 black squares are allowed.
6) No row or column is entirely white or entirely black.
Puzzle of the Week #245 - Three Digits
I have three digits A B C, such that A is less than B, which is less than C. I can arrange these to form six different 3-digit numbers.
When A is at the start, both possible numbers (ABC and ACB) are prime.
When A is in the middle, both numbers are semi-prime (the product of two prime numbers).
When A is at the end, the number is either abundant by 71 (the sum of its proper divisors is 71 more than the number itself), or deficient by 226 (the sum of its proper divisors is 226 less than the number itself).
What are the three digits?