Assemble these two- and three-letter chunks into six surnames of famous people with a specific occupation in common:
ANE BO CH CHA ER ETT
HA ILL LL MM NDE NDL
NES RE RIS SP TIE
Puzzle of the Week #329 - p+2=sp
I have a number, n, for which it is true that whenever a semiprime is 2 greater than a prime, they are either both factors of n, or neither are. A semiprime is a number with exactly two prime factors, for example 4 (2x2) or 6 (2x3).
So for instance, 33 is a semiprime (3x11) which is 2 greater than a prime (31), and so EITHER 33 and 31 both divide into n, OR neither do.
My number only has one pair of repeated prime factors: a pair of 3s. All its other prime factors are unique.
n is the smallest possible number to satisfy the above rules. What is n?
For an extra challenge, what is the next smallest number that satisfies the rules?
Puzzle of the Week #328 - Binary Determination
Place either a 0 or a 1 in each empty square such that each row and each column will form a correct multiplication of two binary numbers to give the decimal number at the end of the row or column. For instance, if the product is 12, the row might read 011x100 (3x4), or one of a number of other possible combinations. I have provided decimal-to-binary tables to help you. Here are two puzzles, one with binary numbers of up to three digits, and one up to four digits.
Puzzle of the Week #327 - False Conjecture
The sequence: 1, 21, 321, 4321, etc is very simple to generate. It is the sum of k(10^(k-1)) for all k between 1 and n, with the results of n=1, 2, 3, 4 shown above. It only gets slightly messier when n is in double digits, for instance the 14th number in the sequence is: 14320987654321, and the 28th number is 30987654320987654320987654321.
It was conjectured that no number in this sequence is prime, but that turns out to be false.
Can you find the first counterexample? Just to warn you this cannot be done without a computer.
Puzzle of the Week #326 - Inch Centimetre Prime
I am thinking of a distance, less than 200m, which is an exact whole number of inches and also an exact whole number of centimetres (one inch is precisely 2.54cm).
The number of inches is one more than a prime number.
The number of centimetres is one more than a prime number.
The sum of the number of inches and the number of centimetres is also one more than a prime number.
What is the distance?
Puzzle of the Week #325 - Uprooted
If (x times the square root of y), plus (y times the square root of x) is 14,
and (x times the square root of x), plus (y times the square root of y) is 22
What is the value of (x plus y)?
Puzzle of the Week #324 - Number Hunt
Can you find a seven-digit number containing seven different digits, whose prime factors are four two-digit primes containing between them eight different digits?
Puzzle of the Week #323 - Triangle Rectangle 2
This is quite similar to PotW #320 but differs in a couple of respects. Firstly, the rectangle is a slightly different height. Secondly, the point F no longer needs to lie on CD, but is free to be anywhere, subject to the other conditions (that ABCD is a rectangle, AEF is a right angle, and E lies on BC.
What is the minimum that DF could be?
Puzzle of the Week #322 - Number Hunt
I have a number, let’s call it n. n doesn’t have any repeated prime factors. For every prime number p, p divides into n IF AND ONLY IF p-1 also divides into n.
For instance, if 23 divides into n, then 22 does also, and if 59 doesn’t divide into n, then neither does 58.
What is the value of n?
Puzzle of the Week #321 - Missing Digits
What are the missing digits in this product of fractions?
Puzzle of the Week #320 - Triangle and Rectangle
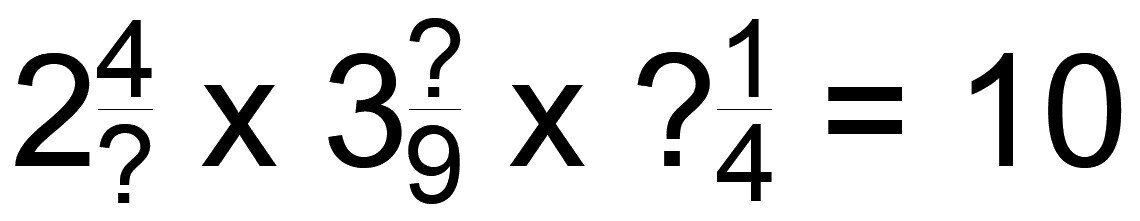
A rectangle ABCD has width 64 and height 80. A right-angled triangle AEF is drawn as shown. What is the minimum that DF could be?
Puzzle of the Week #319 - Power Sum Palaver
w + x + y + z = 2
w^2 + x^2 + y^2 + z^2 = 2
w^3 + x^3 + y^3 + z^3 = -4
w^4 + x^4 + y^4 + z^4 = -6
What is the value of: w^7 + x^7 + y^7 + z^7 ?
Puzzle of the Week #318 - Highest Prime Factors
What is the lowest number n such that if a is the highest prime factor of n, then b (not equal to a) is the highest prime factor of (n-a), and c (not equal to a or b) is the highest prime factor of (n-a-b)?
For instance, a higher example is 700. The highest prime factor of 700 is 7, the highest prime factor of 693 is 11, and the highest prime factor of 682 is 31.
Puzzle of the Week #317 - Ships That Crash in the Night
There are two ships, a fast one and a slower one, each travel consistently at their own fixed speed.
If the fast ship travels in a straight line from Duxmouth to Boxcote and the slow ship travels from Axton to Caxcombe, and they each set off at the same time, they will collide where the routes cross.
Similarly, if the fast ship travels in a straight line from Caxcombe to Axton and the slow ship travels from Boxcote to Duxmouth, and they each set off at the same time, they will again collide where the routes cross.
If the fast ship travels from Caxcombe to Duxmouth and the slow ship from Axton to Boxcote, and they set off at the same time, clearly they won’t clash, as the routes don’t cross, but which ship will reach its destination first?
Puzzle of the Week #316 - Galaxy Quest
It's been a while since I invented a new puzzle type, although this one is a combination of a couple of ideas already around in puzzle world.
Your task is to subdivide the grid into regions, such that every region has 180-degree rotation symmetry. (They might also have 90-degree symmetry and/or reflective symmetry, but this is not necessary).
Every square that in the solved grid is bordered by 2 or fewer lines, is denoted by the number of lines bordering it. Any square that will have 3 or 4 lines bordering it, is left blank.
The only other rule is that you can't have two single square regions next to each other, hence why the top right corner of the example must be a pair.
Puzzle of the Week #315 - Shaded Area
In this figure, the shaded area is in between an isosceles triangle with sides 1, 1 and x, and an equilateral triangle with sides x.
If x is close to zero, the isosceles triangle becomes very thin and the shaded area in very small.
If x is close to 1, there is very little difference between the isosceles triangle and the equilateral triangle, and again the shaded area is very small.
In between, the shaded area is at a maximum. For what value of x is this the case?
Usually I like to engineer these puzzles so that the solution is a whole number, however this is not possible in this case, but the exact solution can be expressed quite concisely. A numerical solution is also acceptable to, let’s say, four decimal places.
Puzzle of the Week #314 - Digit Sums
The longest streak of consecutive numbers, NONE of whose digit sums is a multiple of 7, is 12 in a row. For instance:
994, digit sum = 9+9+4 = 22, remainder after division by 7 = 1
995, digit sum = 9+9+5 = 23, remainder after division by 7 = 2
996, digit sum = 24, remainder after division by 7 = 3
997, digit sum = 25, remainder after division by 7 = 4
998, digit sum = 26, remainder after division by 7 = 5
999, digit sum = 27, remainder after division by 7 = 6
1000, digit sum = 1, remainder after division by 7 = 1
1001, digit sum = 2, remainder after division by 7 = 2
1002, digit sum = 3, remainder after division by 7 = 3
1003, digit sum = 4, remainder after division by 7 = 4
1004, digit sum = 5, remainder after division by 7 = 5
1005, digit sum = 6, remainder after division by 7 = 6
By the same notion, the length of the longest streak of consecutive numbers, NONE of whose digital sums is a multiple of 13, happens to be an exact multiple of 13 itself.
How long is the streak, and can you find an example?
Puzzle of the Week #313 - Alien Number System
Imagine a number system where the only numbers are those that are 1 greater than a multiple of 20, for instance, 21, 81, 1741. You cannot add or subtract using this number system without the result being a number outside the number system, however it is possible to multiply, as multiplying together two numbers that are each 1 greater than a multiple of 20 will result in a third number that is also 1 greater than a multiple of 20. For example, 21 x 61 = 1281.
‘Prime’ numbers exist in this system, defined as numbers that cannot be formed by multiplying together two smaller numbers in the number system. All actual primes, such as 41, are obviously still prime in this system, but other numbers, such as 21 or 81, are not prime usually, but are in this system.
One well known fact about ordinary numbers is that they are the product of prime numbers in exactly one way, for example 72 = 2x2x2x3x3. However, it is possible for numbers in this special number system to be the product of ‘prime’ (within the system) numbers in more than one way.
What is the smallest number in this number system that is the product of ‘primes’ in two distinct ways?
Puzzle of the Week #312 - Wolf Tooth
A Wolf Tooth cube is a strange and interesting puzzle. It is almost like solving two puzzles at once. In essence it is a cube and an octahedron intersected. Each of the six cube faces has one of the octahedron vertices in the centre, a square based pyramid with four different colours on it. Each of the eight octahedron faces has one of the cube vertices in the centre, a triangular based pyramid with three different colours on it.
The arrangement of colours on the cube part are as follows:
Red is opposite Orange
White is opposite Yellow
Blue is opposite Green
Red White and Blue appear clockwise on their shared vertex
The arrangement of colours on the octahedron part are as follows:
Red is opposite White
Yellow is opposite Silver
Purple is opposite Blue
Orange is opposite Green
Red Yellow Purple and Orange appear clockwise around their shared vertex
It is possible to orient the octahedron through the cube such that none of the same colours on the cube and octahedron are in contact?
If so what four colours appear on the octahedron vertex in the middle of the green cube face?
To illustrate the objective of the puzzle, in the cube above the white cube face and the white octahedron face are not in contact, whereas the green cube face and the green octahedron face are in contact, which is not permitted within this puzzle.
(For the purposes of this puzzle I have changed the order of the colours on the octahedron part from the colouring on an actual Wolf Tooth cube, shown here.)
Puzzle of the Week #311 - Diamond Ring
ABCD is a square with side length of 2, rotated through 45 degrees so that the diagonal BD becomes horizontal. A circle of unknown radius is drawn through B and D as shown. Within the large circle two further circles are drawn, respectively above and below BD, and the maximum size they can be whilst staying within the large circle.
The region that lies within the large circle but outside of the two smaller circles is shaded.
What is the area of the shaded region?
