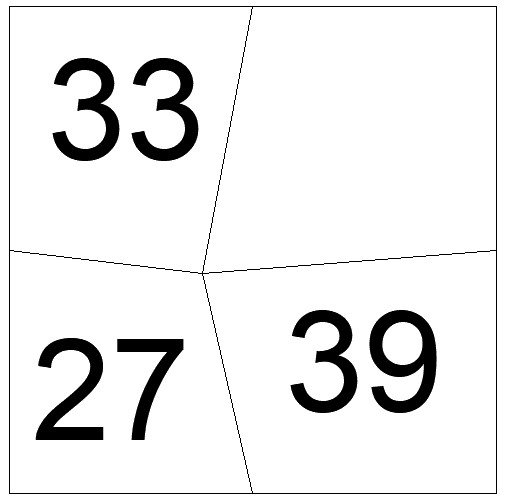
Four lines are drawn from the midpoints of four sides of a square to a point in the interior, dividing the square into four regions. The areas of three of those regions are given. If the bottom left point is at (0,0), what are the coordinates of the interior point?
Puzzle of the Week #412 - Quad in a Quarter
What is the area of this quadrilateral, drawn in a quarter circle?
Puzzle of the Week #411 - Best Remakes
Watching the Oscars this year I noticed that one of the nominees for Best Picture was a remake of one of the very first winners almost a century ago. In fact, in four of the last five years, a Best Picture nominee has been a remake of a film to previously be nominated for Best Picture. I trawled the lists and found several more examples for you to try and discover below. Where a film has three or more words in the title, I’ve given the initials; where it has only a single or two-word title, I’ve given an anagram.
Winner 1930, nominated 2022: AQOTWF
Winner 1961, nominated 2021: WSS
Nominated 1933 and 2019: TIME NOT WELL
Nominated 1937 and 2018: ASIB
Nominated 1935 and 2012: SMELLIER BASES
Nominated 1952 and 2001: GERONIMO ULU
Nominated 1943 and 1978: HCW
Nominated 1936 and 1968: RAJ
Nominated 1934 and 1963: ACE PATROL
Winner 1935, nominated 1962: MOTB
Puzzle of the Week #410 - Six Starfish
Enter the letters E, N, I, G, M and A into the circles at the end of the starfish tentacles, so that:
Each starfish will have each letter once each.
Each straight line (indicated by an arrow) will have each letter once each.
Each triangle (indicated by a bold line) will be surrounded by each letter once each.
Puzzle of the Week #409 - Classes
A school year is split into three equal classes. Every student either is either a boy or a girl, with the total number of boys and girls being equal.
Class A has twice as many girls as class B, and four times as many boys as class C.
Class C has two more girls than class B has boys.
How many students are there altogether?
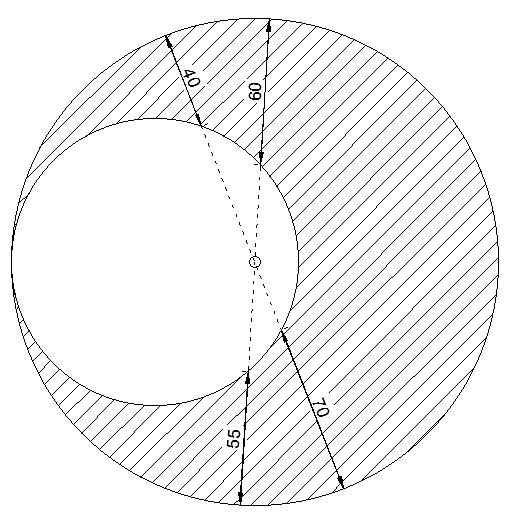
Puzzle of the Week #408 - Eclipse
One circle is tangent to the inside of another circle as shown. Two diameters of the larger circle pass behind the smaller circle, and the exposed sections of the lines measure 40, 60, 70 and 55 respectively.
What is the area of the shaded region?
Puzzle of the Week #407 - Strange Area Dissection
I’m writing this before publishing last week’s puzzle, so it’s possible you used a dissection to establish the area already, in which case you have possibly already solved this one too.
Still using the same shape from the last puzzle; we previously discovered that the area was exactly 1. This being the case it ought to be possible to dissect the shape into a number of pieces and reassemble those pieces to form a unit square. For instance, below is a method using five parts, but what is the fewest number of pieces with which you can achieve this?
Puzzle of the Week #406 - Strange Area
I have a shape as below: a concave pentagon. Two of the points are the ends of the base of a unit semicircle. Two other points lie on the semicircle; at those points the angles are right angles. Four of the five edges are equal in length, and the fifth length (being the base of the semicircle) is equal to 2.
What is the area of the pentagon?
Puzzle of the Week #405 - Number Hunt
What is the largest prime number that CANNOT be expressed as the sum of three positive composite odd numbers?
Puzzle of the Week #404 - Points on a Circle
A, B, C and D are four points on a circle. Lines AC and BD cross at E.
AB=10, BC=10, BE=4.
What is the length of ED?
Puzzle of the Week #403 - Triple Duality
The answer to each clue is a 3-, 6-, or 9-letter word. If you split these into 3-letter chunks, you will find 20 different ‘triples’ each appearing twice.
For example if one answer was ‘bellow’ then ‘bel’ and ‘low’ would appear somewhere else too, for instance in ‘disbelief’ and ‘lowest’, but then ‘dis’, ‘ief’ and ‘est’ would have to appear somewhere else too, etc, until all triples have appeared exactly twice.
100% probability
A group of related objects
A mongrel dog
Bunk or flower?
Chicken leg used in percussion?
Conducted or escorted
Corruptly paid money
Cut short
Dictionary of synonyms
Fourfold
Lots
More repulsive
Old name for Sulphur
Recite or chant in monotone
Reddish brown apple colour
Slang for a police officer
Small plate for a kitten's milk
The definite article
Whimsical
Xerox machine
Puzzle of the Week #402 - 402 Puzzle
(A+B) + (AxB) = 402. A and B are positive whole numbers. What is A + B ?
Puzzle of the Week #401 - Chunkwords: Mathematical
I have taken ten 9-letter mathematical terms and split them into 3-letter chunks. Can you reassemble them?
AIN ALG AME ANG ANS BLE COT DER DIV DOD
DRA ECA ENT ERA EXP GON ION ISI NSF NUM
ORI ORM PAR QUA REM TER THM TIC TOR TRA
Puzzle of the Week #400 - Peace Treaty
To celebrate reaching 400 Puzzles of the Week, I thought I’d bring out one of my favourite puzzles. This one first appeared in my book ‘Paddocks’ available from lulu.com or amazon.
On the island of Honeycombia live two warring tribes: the Crosslanders and the Noughtlanders. They have stopped fighting for now, but a permanent ceasefire is in your hands.
It is your job, as chief peace negotiator, to divide the island in a way that satisfies both tribes.
Each tribe wants their own territory to be in one piece, so that they can travel from any point in their own territory to any other, without crossing the other tribe's territory, and without going to sea.
Also, neither tribe wants the other to be able to build certain types of structure: a diamond mine would require four hexagons together in a diamond shape, and a car factory would require five hexagons together in an axle shape. Consequently neither shape can appear on the island, in any orientation, for either tribe.
Oddly, neither side seems to care who ends up with more territory, as long as all of the hexagons are assigned to one of the two tribes.
Both tribes have already laid claim to some areas of the island. Can you assign all of the other hexagons to one or other of the tribes, so that a lasting peace can emerge on Honeycombia?
Hint: each tribe can only have one length of coastline. If the coastline switched back and forth between the two tribes, it wouldn't be possible for one territory to be in one piece without dividing the other territory in two.
Puzzle of the Week # 399 - What's Wrong
In the following figure, O is the centre of a circle, AB is tangent to that circle, CD is parallel to AB, C and D lie on the circle, C also lies on AO.
Two angles are marked, but are they correct, and if not, why not?
Puzzle of the Week #398 - Find The Radius
A circle is inscribed within a quarter circle. A line of length 1 extends from the vertical edge to the arc of the quarter circle is parallel to the horizontal edge of the quarter circle, and tangent to the inscribed circle.
What is the radius, R, of the quarter circle?
1 point for a numerical solution, 2 points for an exact solution using nested square roots, 3 points for finding a quartic polynomial whose real positive solution is R.
Puzzle of the Week #397 - Starting Squares
I have an 11-digit square number.
The first six digits also form a square number.
The number formed by the first three digits is a square number.
The number formed by the first two digits is a square number.
The first digit is a square number.
What is the number?
Puzzle of the Week #396 - Square in a Quarter Circle
A tilted square is in a quarter-circle as shown, such that three of the four corners of the square lie on the quarter-circle. The point on the left where it does so, is 120 from the bottom corner of the quarter-circle and 121 from the top corner.
What is the area of the square?
Puzzle of the Week #395 - Vaguely Defined Pentagon
A pentagon has side lengths that are five consecutive whole numbers, arranged in numerical order around the pentagon.
Three of the internal angles of the pentagon are right angles.
What is the area of the pentagon?
Puzzle of the Week #394 - Coin Paradox
I’m thinking about a sequence of coin flips resulting in either heads or tails, with equal probability. Which of the following statements are true?
In a game where I win if we flip HTH on consecutive throws and my friend wins if we flip HTT on consecutive throws:
1) If we just toss the coin three times in succession, we each have an equal probability of winning (although most of the time neither of us would win).
2) If we keep flipping until either HTH or HTT comes up, we will win the game with equal probability.
3) If we keep flipping until either HTH or HTT comes up, the average number of flips it will take is on average the same, whether I win or my friend does.
4) If we each have our own coin, and I keep flipping until I see HTH on consecutive flips, and my friend keeps flipping her coin until she sees HTT on consecutive flips, we will both take the same number of flips on average.