Each person+place contains the five vowels exactly once each. Caroline is only missing the letter U so she is from Hull (or anywhere else with a ‘u’ and no other vowels).
Solution of the Week #241 - Irregular Polyhedron
Using Euler’s formula for vertices, edges and faces of a polyhedron:
V+F-E = 2
If we let the number of pentagonal face be n, then the number of faces is (n+2), the number of edges is (14+5n)/2 (since each edge belongs to two faces), and the number of vertices is (14+5n)/3 (since each vertex belongs to three faces).
(14+5n)/3 + (n+2) – (14+5n)/2 = 2
Which boils down to n = 14, so there are 14 pentagonal faces.
Below is such a polyhedron. All of the edges and all of the vertices are visible, just one heptagonal face is on the far side.
Solution of the Week #240 - Base 4 Code
1-103 113-11 1-13-11 113-11 12-21-32-10 113-11 1-102-11 32-33-110 32-11-1-102-30-121 1-103 113-21-103-11 1-103 113-11 20-33-100-11-10 110-33 2-11-3-33-31-11.
“As we age we find we are not nearly as wise as we hoped to become.”
(I deliberately wrote a sentence that would result in ambiguous words, as ‘we’ and ‘age’ both encode to 11311).
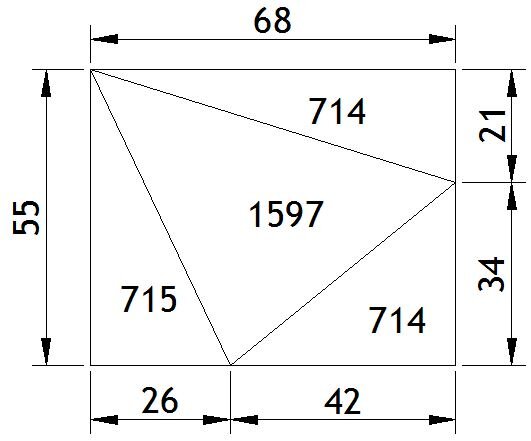
Solution of the Week #239 - Nearly Equal Corners
x is 714. One possible set of dimensions are as below:
My expectation being that the solver would try some numbers and arrive at this or another integer solution. However it is solvable using algebra as below (excuse my handwriting):
Alternatively, there is a far quicker way to arrive at an approximate solution by looking at a similar but easier problem:
Solution of the Week #238 - Circle Box
A score of 100(pi) is possible: (36+25+16+9+4+10).
If you’re interested, I also did this for a 100x100 grid, which results in a score of 44246(pi), shown below.
Solution of the Week #235 - Shaded Area
Solution of the Week #225 - Six Integers - submitted by Simon Richards
The first challenge is to spot the neat trick.
1 The first equation
X^2 = A^2 + 4B + 1
Consider (A + 1)^2 will equal A^2 + 2A + 1
Hence if we solve for X being 1 + A then 4B +1 = 2A + 1 Hence A = 2B (This is the neat trick)
2 We now need to discount X being A + n where n is greater than 1.
If n = 2 then A^2 + 4A + 4
the 2B +1 = 4A + 4 hence 2B = 4A + 3 this can be discounted as B would be greater than A.
3 The second equation using the same logic as above B = 2C
4 Hence A = 2B = 4C
5 Then start with the third formula find the value of Z^2 which has an integer square root.
6 Then do the same with the other equations.
7 The answer is C = 24, B=48 and A=96 giving Z=31, Y=49 and X-97
8 NOTE there is almost but not quite another solution C, B, A = 4, 8 ,16 give Z, Y, X = 8, 8, 17.
Solution of the Week #211 - Angle
45 degrees
ACE forms a right angled isosceles triangle
Solution of the Week #180 - Letter Wall - submitted by Philip Morris Jones
There are 26 letters and you draw 2 at random so the first letter is one of 26 and the second one of 25 so there are 26*25 = 650 ways to pick two letters.
The letter A is adjacent to B and H so that is 2 ways to pick adjacent letters with A as the first letter.
B is next to 4 letters so there are 4 ways to pick adjacent letters with B as the first, and AB is different to BA.
If you go through the wall you get the following ways per brick
2 4 4 4 4 4 2
5 6 6 6 6 5
3 6 6 6 6 6 3
3 4 4 4 4 3
and that sums to 116 so you get 116/650 which simplifies to 58/325
Solution of the Week #178 - Tangent Curve
The missing radius is 11.
Solution of the Week #177 - Skyscrapers and Empty Lots
Solution of the Week #176 - Nine Point Circle
The points are nine of the twelve vertices of a regular dodecagon (12-sided polygon).
Solution of the Week #175 - Out Standing In My Field
Solution of the Week #174 - Rectangular Area
506
23√2 x 11√2
Solution to Puzzle of the Week #145
The probability of the centre of the circle being within the pentagon is 11/16.
The general formula for an n-sided shape is: 1 - n/(2^(n-1))
If you're interested, the derivation of the above formula is as follows:
The puzzle asked, for five points positioned at random, what is the probability of the pentagon formed by them containing the centre of the circle.
Let’s switch is round and ask what the probability is of missing the centre. For this to be the case, all of the points must be in the same half of the circle, but that half could be 0 to 180 degrees, or 180 to 360, or 63 to 243, or any of the countless other ways. So let us pick a point, one of the five random points, and (temporarily) call that our zero, our datum. What is the chance of the other 4 points being less than 180 degrees clockwise from the datum? Simply ½ x ½ x ½ x ½, or 1/16.
Each of the five points can be taken as the datum in turn. So is it just a matter of adding together those five probabilities (or, as they are equal, simply multiplying 1/16 by 5)? Well yes, since at most one datum can result in all the other points being less than 180 clockwise from that point, the five cases are mutually exclusive, and it is indeed just a matter of adding them together.
From here it is easy to see what the general equation is. For n points, the probability of not containing the centre is:
n/(2^(n-1))
Giving the sequence ¾, 4/8, 5/16, 6/32, 7/64, 8/128 etc (before simplification, to demonstrate that the numerator increases by one and the denominator doubles with each new term)
Then the probability of containing the centre is merely the complement of this, or 1 – n/(2^(n-1))
Resulting in the sequence ¼, ½, 11/16, 13/16, 57/64, 15/16 etc.
Alex Bellos' 'Can You Solve It?' Guardian Column
I'm delighted that the maths/puzzle writer Alex Bellos has used some of my puzzles in his Guardian column.
https://www.theguardian.com/science/2017/may/08/can-you-solve-it-have-a-punt-on-the-paddocks-puzzle
Thanks Alex!
Solution of the Week #89 - To the Right - submitted by Roisin Carters
Christian Festival = EASTER Food tester = TASTER
Annoy = BOTHER Parent = MOTHER
Childminder = SITTER Better adapted = FITTER
In each of these cases, the initial letter has ‘lurched’ two places to the right on a QWERTY keyboard.
So speak/complete = UTTER Animal = OTTER
Solution of the Week #80 - Total Digits - submitted by Roisin Carters
The number I am thinking of has to contain at least five digits, as for any smaller number the total number of digits I write down cannot be exactly four times my number, as many of the numbers only contribute one to three digits each.
The total number of digits I write down up to 9,999 = 9 x 1 + 90 x 2 + 900 x 3 + 9,000 x 4 = 38,889
The total number of digits up to my number n, is therefore 38,889 + 5(n – 9,999) which must equal 4n.
Rearranging this equation gives 5n – 11,106 = 4n and so n = 11,106.
Solution of the Week #76 – Dice Bingo – submitted by Kjell Jonasson
Let the die be symmetric and have n sides. As you start and keep rolling it you progress step by step, from having seen k-1 top sides to having seen k top sides, k running from 1 to n. The step from k-1 to k takes, on the average, n/(n-k+1) rolls. The total number of rolls required to having seen all the n top sides is, on the average, nx[1/n+1/(n-1)+1/(n-2)+...+1)].
For n=20 the sum is almost exactly 72. Hence the die is a regular icosahedron!
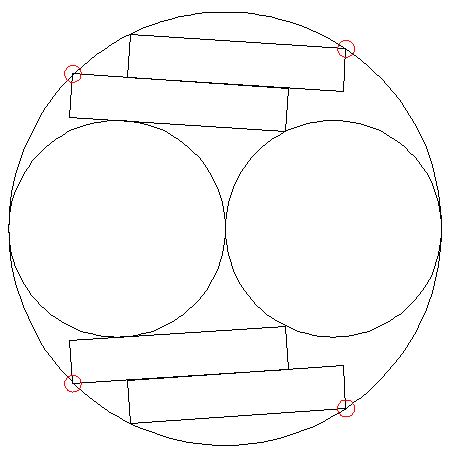
Solution to Puzzle #75 - Snack-a-Jack-in-a-Box
A few of you (those I gave a mention to on the Facebook post) correctly supposed that the best approach was to have two piles of five rice cakes each, and then place the other four, two in each of the spaces left over.
The surprising detail that no-one managed to provide, is that technically they don't fit! There is a very slight overlap - a fraction of a millimetre - at the four points shown in the diagram below. Had the rice cakes been just 1.9cm thick, there would have been no problem (and in fact real Snack-a-Jacks are slightly shy of 2cm thick anyway).
For any practical purposes they do fit, which is why I was happy to accept that answer if the arrangement was optimal.