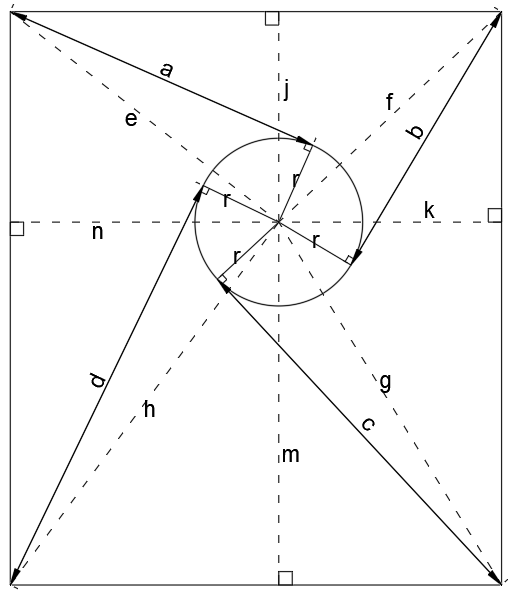
Looking at the general case above, each tangent line a,b,c,d is by definition at right angles to the radius of the circle, r, so we can define a,b,c,d in terms of e,f,g,h,r using Pythagoras:
a^2=e^2-r^2
b^2=f^2-r^2
c^2=g^2-r^2
d^2=h^2-r^2
We can then also define e,f,g,h in terms of the perpendicular distances from the centre of the circle to the edges of the rectangle j,k,m,n:
e^2=j^2+n^2
f^2=j^2+k^2
g^2=k^2+m^2
h^2=m^2+n^2
Next I’m going to use the above to find an expression for a^2+c^2:
a^2+c^2=j^2+n^2+k^2+m^2-2r^2
And also for b^2+c^2:
b^2+d^2=j^2+k^2+m^2+n^2-2r^2
Both these are equal to the same thing, so a^2+c^2=b^2+d^2
Returning to the numbers in the puzzle:
10^2+15^2=6^2+?^2
?^2=289
?=17