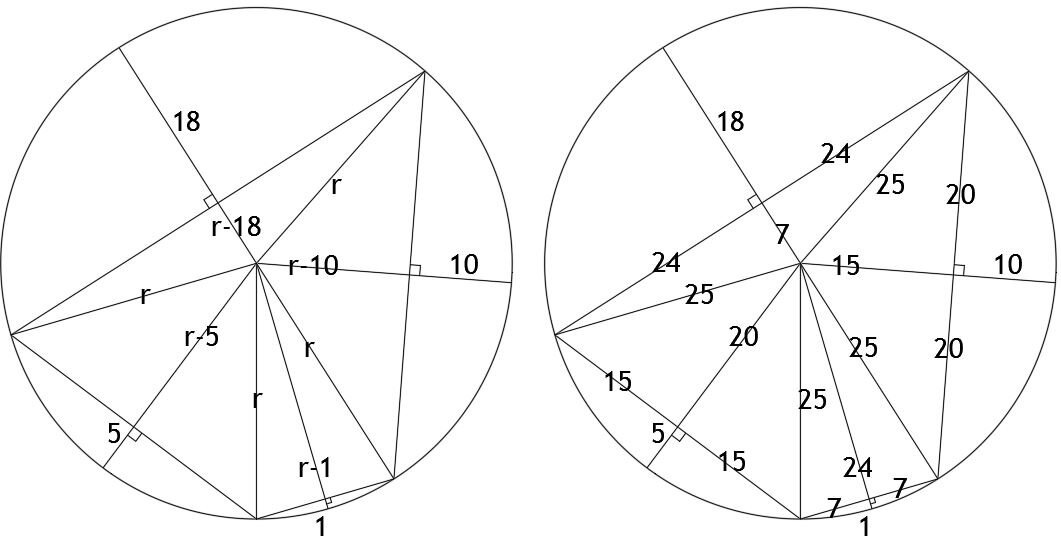
Area = 936.

To work through the problem in trigonometry is a bit of a nightmare so I’d envisage people solving the problem by drawing lines from all vertices and midpoints to the centre of the circle, calculating the cosine of each of the angles at the centre in terms of ‘r’, and then varying the value of r until the angles add up to 180 degrees. This occurs when r is precisely 25. From there we can easily work out the side lengths of all 8 of the internal right-angled triangles and tot up their areas to get 936.

If you do that you might be surprised to discover that the eight triangles are two sets of four congruent triangles: (7,24,25) and (15,20,25).