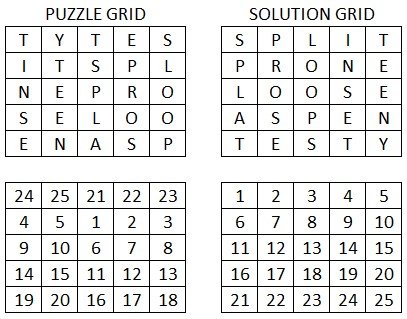
I have taken a square of five letter words and scrambled it in a particular way: each letter was moved across 2 and down 1 from its position in the solution grid, which is made clearer by the corresponding number grid below.

This is a logic puzzle, not a word puzzle, as is apparent from the fact that I’ve given you the solution grid as well as the puzzle grid.

Your task is to figure out the least number of swaps required to turn the puzzle grid into the solution grid, with each swap simply being to take any two letters from anywhere in the grid and swap them.

If you attempted this on the number grid, you would require 20 swaps, however in the letter grid you can take advantage of the fact that some letters are repeated to reduce the number of swaps.

A bonus question if you feel like it, is to work out how many swaps you can make that, while advancing towards to solution within the minimum number of swaps, don’t actually solve any letters. To explain what I mean, in the number grid if you were to swap the 1 and the 15, neither would be in its final position, but you have advanced the solution in the sense that it can now be solved in 19 further swaps.