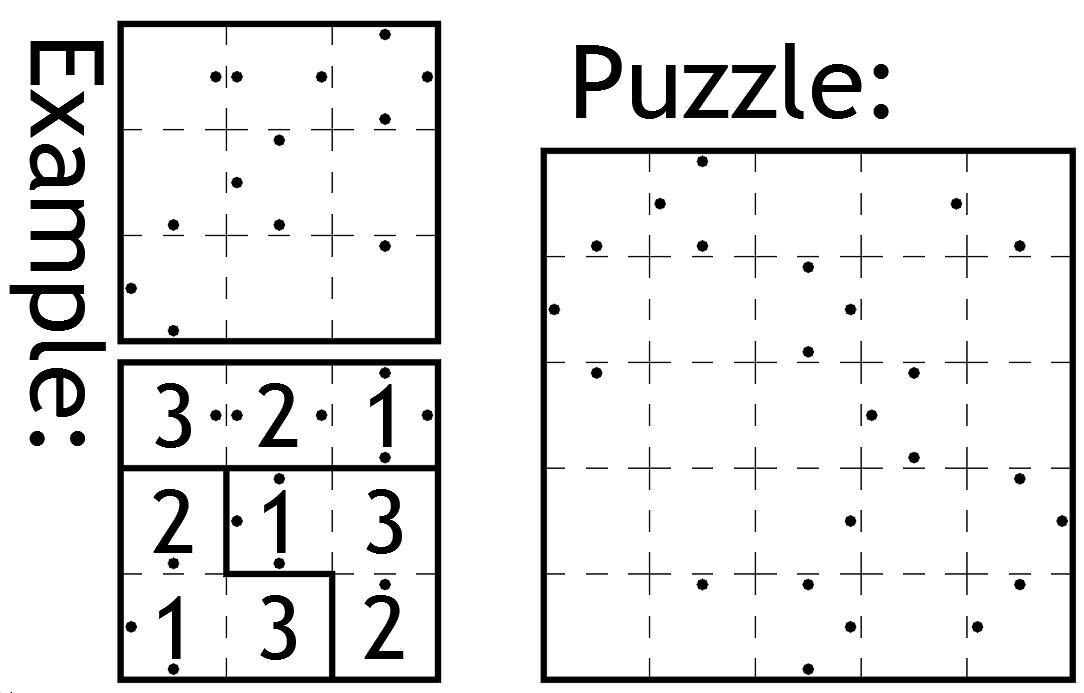
Your task is to solve this irregular sudoku (the digits 1 to 5 appearing once each in every row, column and 'shape').
Except that I haven't told you where the boundaries between the shapes are; instead I've placed dots in any square where the number to be placed in the square denotes how many squares (including the one with the dot in) until you get to the next boundary line in the direction of the dot.
Clear as mud? Hopefully the attached example 3x3 will help. For instance, the 2 in the middle of the top row, combined with the left and right dots, says that in each direction left and right from that square there are two squares (including the one with the 2 and the dots in) before you get to a boundary line (which happens to be the outer boundary of the entire grid).
In both the example and the puzzle, I have placed dots in every position that I could, according to the rules.
A hint to get you started: if a dot appears next to the outside boundary of the grid, then that square must contain a 1.