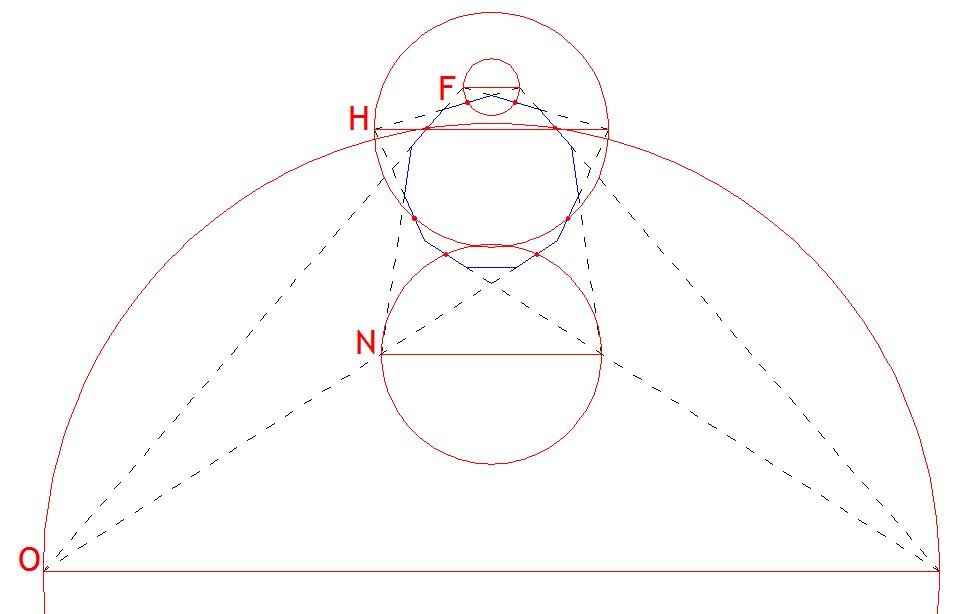
Lines F, H, N and O are all diameters of circles which pass through midpoints of sides of the original hendecagon.

The key insight is that an angle within a semicircle will be a right angle, so we start off with two construction lines at right angles, one collinear with one of the sides of the 11-sided polygon, another passing through the vertex opposite that side. By definition they will intersect at the midpoint of the side of the polygon.

On the left hand side draw extensions from all possible polygon edges that can meet the blue (horizontal) line, and on the right hand side draw extensions from all possible polygon edges that can meet the red (vertical) line (some will go upwards, others downwards). The red intersections are intersection points of extended polygon sides, as the red lines can be mirrored by the red axis. The blue intersections are already intersections of extended polygon sides as the blue axis itself is an extended polygon side.

The intersection points with the main axes can be paired up according to how far they are from the centre of the polygon. By definition any circle with one of these magenta pairing lines as its diameter will pass through the point where the axes meet (as well as a second polygon midpoint which will vary from circle to circle).

None of these pairing lines are horizontal as in the puzzle, but it’s easy to see how for each pairing line, the figure can be rotated such that the line is horizontal. If you do so you will find that the four lines correspond to the lines F, H, N and O in the puzzle.