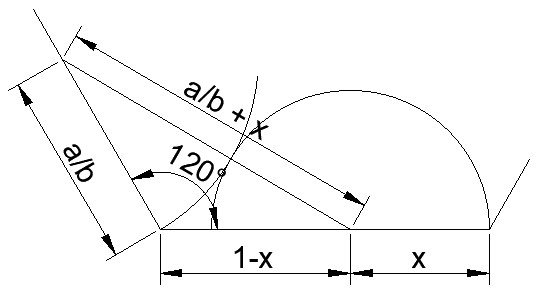
Let’s look at a general case where the previous radius is a/b and we wish to find the next radius x.

Using the cosine rule on the triangle shown, and taking advantage of the fact that cosine of 120 degrees is -0.5, we get:

(a/b + x)^2 = (a/b)^2 + (1-x)^2 + a/b(1-x)

(a/b)^2 + 2ax/b + x^2 = (a/b)^2 + 1 - 2x + x^2 + a/b – ax/b

2ax/b = 1 - 2x + a/b – ax/b

(2 + 3a/b)x = 1 + a/b

x = (1 + a/b)/(2 + 3a/b) = (a+b)/(3a+2b)

so assuming a and b are integers, x will be a rational number.

We can repeatedly use this formula starting from Ra = 1/2.

Rb = 3/7, Rc is 10/23, Rd = 33/76 and finally Re = 109/251. If you are curious, these fractions are converging on a value of

(sqrt(13)-1)/6.