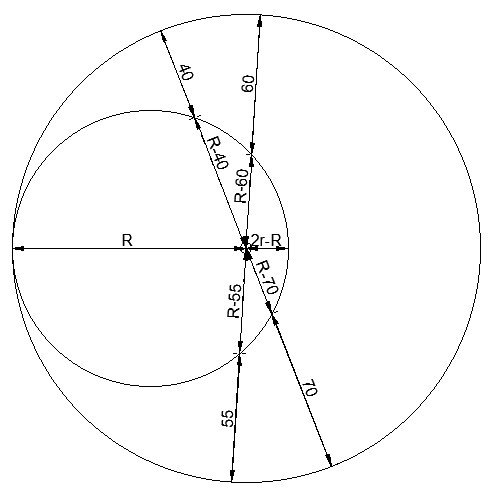
If we call the radius of the large circle ‘R’ and that of the smaller circle ‘r’, then the shaded area is pi*(R^2-r^2).

To first determine R we look at the chords that cross the small circle, then will have lengths of (R-40), (R-60), (R-70) and (R-55). According to the intersecting chords theorem, the product of the opposite pairs will be equal.

(R-40)(R-70)=(R-60)(R-55)

R^2 – 110R + 2800 = R^2 - 115R + 3300

5R = 500

R=100

So each side of the equation (R-40)(R-70)=(R-60)(R-55) will be equal to 1800.

To find r, we can draw a third chord, which goes from the tangent point, and through both centres. The intersecting chords along this line will be R and 2r-R.

R(2r-R) = 1800

200r – 10000 = 1800

r – 50 = 9

r=59

100^2 – 59^2 = 6519. The shaded region is therefore 6519*pi, which is about 20480.