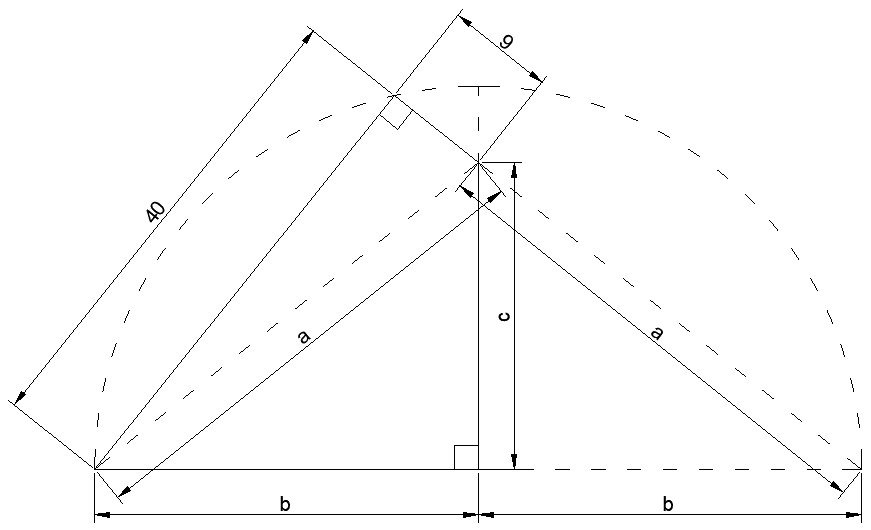
From Pythagoras on the (40,9,a) triangle, the length of a is 41. If we reflect this in the vertical axis we get a line that is collinear to the line of length 9. This gives another right-angled triangle (40,9+a,2b) and using Pythagoras again we find b=5*sqrt(41). Using Pythagoras yet a third time on the (b,c,a) triangle, we find c=4*sqrt(41). Finally to find the area of the quadrilateral we calculate ((40*9)+(b*c))/2, which neatly cancels out the square roots and gives the answer of 590.

Alternatively, the following shortcut means you don’t even have to calculate b or c: notice that the quadrilateral exceeds the 40*9 triangle by the exact same amount that the 40*50 triangle exceeds the quadrilateral. So the quadrilateral will be the average of the areas of the 40*9 triangle and the 40*50 triangle, so (180+1000)/2 = 590.