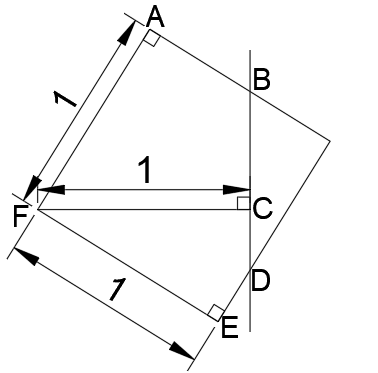
The above figure represents one of the 1x1 squares, and how it interacts with the edge of the 3x3 square represented by the line through BD. Because of the fact that the inner point of the square F lies on a corner of the middle square of the figure we can say that FC is equal to 1 in length. ABCF is a kite, and therefore AB=BC. Likewise CDEF is a kite, and so CD=DE. The overall change to the perimeter from this square is that we lose BD, but gain AB, DE, AF and FE. But BD is just AB+DE so they cancel out, and AF=FE=1, so overall we gain 2. Since there are four such squares, we gain 8 compared to the original 3x3 square which has a perimeter of 12. And so therefore the overall perimeter = 20.