Solution of the Week #262 - Hexagon Area

If you extend two of the lines until they meet, as shown, and then also draw a line from this new point to the point inside the hexagon you will form two new triangles with the same base and height as two of the given triangles. The sum of these, and therefore the area of the quadrilateral, will be 12. But this 12 is also the sum of the other given triangle and the new equilateral triangle formed by extending the lines. This equilateral triangle therefore has an area of 7. This is also one sixth of the area of the original hexagon. The ultimate answer is therefore 42.

Solution of the Week #260 - Semi-grams

ALERT + RATIO = RETAL + IATOR = RETALIATOR

METRO + SENSE = REMOT + ENESS = REMOTENESS

NOTED + ROAST = DETON + ATORS = DETONATORS

TIMES + GIANT = ESTIM + ATING = ESTIMATING

UPSET + SOUND = STUPE + NDOUS = STUPENDOUS

Alternatively you could swap the second halves of DETONATORS and ESTIMATING

Solution of the Week #259 - Triangle Area (Tough)

Imagine a couple of (differently) scaled down versions of the triangle, one where the corner square becomes area 1, and one where the sloping square becomes area 1. From using similar triangles and chasing the angle ‘a’ around the figure we can see that the areas of some of the other parts of the triangle will be the same across the two figures. We can call these triangular areas x, y and z.

(I should probably point out at this point, while I’m introducing lots of new variables, that I’ve no intention of ever calculating what a, x or y evaluate to. z on the other hand…).

Each of the triangles with area x, y or z has one right angle, one angle ‘a’, and one side of length 1. You can express x y and z in terms of trig functions of a:

x = tan(a)/2 ( = sin(a)/2cos(a) )

y = cot(a)/2 ( = cos(a)/2sin(a) )

z = sin(a)cos(a)/2

If you multiply x and y together you get simply xy = 1/4

If you add the reciprocals of x and y:

1/x + 1/y = 2cos(a)/sin(a) + 2sin(a)/cos(a) = 2((cos(a))^2+(sin(a))^2)/ sin(a)cos(a)

But since (cos(a))^2+(sin(a))^2 = 1 by definition:

1/x + 1/y = 1/z

Putting these two facts together we get (x+y)/(1/4)=1/z

4(x+y)=1/z

x+y = 1/4z

Now scaling the two triangles back up so that the square areas are 363 and 336 respectively, and equating the areas of the two triangles we find that:

Area = 363(1+x+y) = 336(1+x+y+z)

Substituting x+y = 1/4z

Area = 363(1+1/4z) = 336(1+1/4z+z)

I’m now going to multiply each term by z and group terms on one side:

336zˆ2 – 27z – 27/4 = 0

Using the quadratic formula we see that:

z = (27 +/- sqrt(27^2 + 27x336))/(2x336)

z = (27+99)/672 (since z is an area and must be positive)

z = 3/16

Plugging that back into one of the area formulae:

Area = 363(1+1/4z) = 363+484 = 847, which is the final answer.

Solution of the Week #258 - Su-Dot-U

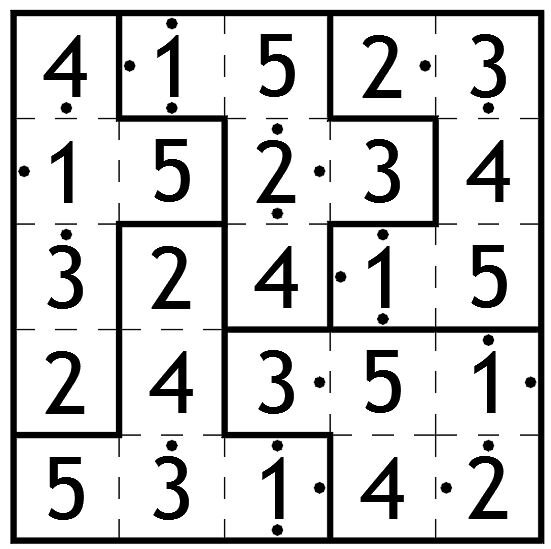
First I used the dots around the edge to place the 1s in the top and bottom rows and first and last columns, allowing me to place some lines and find some places where there are definitely not lines.

Since there are no dots above or below the 1 in the first column, but there is a downward dot in the square above the 1, that square must contain a 3. This means the lower 5 squares of column 1 must be part of the same shape, along with one square from the second column. It must be the one in the second row as if there was a line separating it from column 1, then the dot tells us that square contains a 1, but it can’t as we already have a 1 in the second column. This completes the left hand shape and the dots now tell us exactly which numbers are where.

Similarly the third square on the top row must be a 3, one square from the second row must complete that shape. Since the squares in the third and fourth columns would lead to a second 1 in that shape, it must be the square in the fifth column. Using the dots and the numbers that have already been placed, the top shape can also now be fully filled in.

The two remaining 1s can now be placed. The 1 in the fifth column is interesting because the lack of dots tells us it is open on three sides. This effectively gives us the entire shape. We can place the 5 in this shape too, to complete the top row.

The dotted square in the fourth row cannot be a 1 as 1s are already present in that column and row. It also can’t be greater than 2 as there is a line in place 2 below it. It must therefore be a 2. The square two above it can only now be a 4. That and a 3 at the end of the second row complete that row.

The final two dotted squares are confirmed to contain a 2 and a 3 respectively. Through normal Sudoku rules the remaining numbers can be placed in the top right shape. We can therefore complete the last two columns.

Since there are two 2s in close proximity in the bottom right corner they must be in different shapes. The one on the bottom row must have lines above and to the right. The bottom right shape must extend a further square above the 3 on the bottom row, but cannot extend further in that direction as it would disrupt the 2 in the third column. We can therefore complete the lines of this shape, and now there is only one way to extend the middle shape without splitting the bottom shape into two pieces. All lines have now been placed.

The 3 and 5 in the third row can be placed since if it were the other way around there would be a dot in the 3 square. The 6 then completes this shape. This disambiguates the 5 and 6 in column four which means completing the second column is now straightforward.

Solution of the Week #257 - Two Squares

There are a few ways of solving this but the most intuitive is probably to dissect the figure into identical triangles and then simply count them. There are 18 in the tilted square and 16 in the lower square, so therefore their areas are in a ratio of 9:8.

Solution of the Week #256 - Su-Dot-U

I start by using the dots at the edge of the grid to place the 1s in the first two rows and the bottom row, and the extra lines that that leads to. This fully determines the shape of the top left region, so I am also able to place the 2 in the top row. The 2 can also be placed in the second row, and the lower line from this fully determines the shape of the top right region. I can now use the dots to place the 2 in the third row, and the lower line from that. The remaining two 1s can be placed, along with the extra lines they tell us. It is now straightforward to place all of the other lines. This fixes the 2, 3 and 4 of the lower right shape (and so therefore also the 5). The final 2 can be placed in the bottom corner. The dot tells us the position of the 3 in the backwards L region, and the lack of dot tells us where the 3 goes in the S region. The last two 3s can now also be placed. From here on in, there is always a row, column or shape that only needs one more number to be complete.

Solution of the Week #255 - Three Squares in a Triangle

I don’t know if having a related puzzle last week is a help or a hindrance, as my approach to solving, for what it’s worth, is not at all similar to last week.

I notice that the given areas are each the sum of two squares (5=4+1, 8=4+4, 17=16+1). In general, if the area is a^2+b^2, then it’s at least possible that each side of the square is a units in one direction, and b units in a perpendicular direction.

On a hunch I hopefully set out lattice points of a coordinate system, and sure enough, each of the corners of each of the squares lies exactly on a lattice point. It is then straightforward to work out what the coordinates of the triangle corners are and then calculate the area of the triangle is 64.

Solution of the Week #254 - Three Squares in a Hexagon

To make life easier we can divide each of the areas by two, (as long as we remember to multiply the final answer by two to compensate). The reason this makes things easier is that the areas will then be square numbers, and therefore the lengths of the edges of the squares will be whole numbers, namely 10, 9 and 17.

Consider the area of the triangle in the very centre. Knowing the lengths we can find the area using Heron’s formula:

A^2 = s(s-a)(s-b)(s-c), where s is the semiperimeter (a+b+c)/2

The area works out to be 36.

Now consider the triangle between the top two squares. The area sine rule states that the area of a triangle is half the product of two adjacent sides, multiplies by the sine of the angle in between. At the moment we don’t know the sine of angle a. In fact I have no intention of calculating it!

I’m going to use the fact that the sine of an angle (a) is the same as the sine of 180-a. This is because the sine graph between 0 and 180 forms a symmetrical curve centred on 90. Any two angles adding up to 180 (or to put it another way, averaging 90) will have the same sine.

Now if we look at angles a and b, they are a full 360 less two right angles (the corners of the squares), and so therefore will add up to 180. Sin a = sin b. Angle b is also between two lengths of 10 and 9. We can therefore see that the area of the top triangle is identical to the area of the middle triangle, which we already know to be 36.

We can use the exact same reasoning to show that the other two triangles are also 36.

Therefore the area of the whole hexagon is 100+81+289+(4x36), and not forgetting to double the answer to get the final answer of 1228.

Solution of the Week #252 - Hexagon Angle

To start with we can assume each side of the hexagon to be 1 unit without affecting the size of the angle. Now work out the lengths of the lines AG and AH using Pythagoras (having first worked out the horizontal and vertical components of each). It transpires that both AG and AH are equal to sqrt(7)/2 (~1.323). This alone is not of much use in working out the angle in question, however if we now calculate the length of the dashed line GH we discover that this too has a length of sqrt(7)/2. Therefore AGH is an equilateral triangle, and the angle we seek is 60 degrees.

If you’re interested about how I created this puzzle, it is a special case of an interesting theorem I stumbled across: if you have three non-overlapping chords of length x, inside a circle of radius x, and then you connect the ends of those chords to form three new chords (which now don’t necessarily have to be x long), then the midpoints of those new chord form an equilateral triangle.

In my puzzle, the x length chords are AB, CD and FA. The fact that the circumscribed circle has radius x is implicit in the fact that those chords are part of a regular hexagon. Therefore the midpoints A, G and H form an equilateral triangle.

Solution of the Week #251 - Trispace

a=39

Below is the figure fully dimensioned.

Quite interestingly, in all cases the total of the three trapezoid perimeters will equal 5a+b. Since in this case the total was 198, and a=13b, this provides a useful shortcut to the fact that b=3 and therefore a=39 (although of course deriving this fact is more work in the short term).

Despite the fact that you don’t need to calculate the lengths of each of the trapezoids, there is only one figure which satisfies the conditions.

Solution of the Week #250 - Squarespace

There are just the right degrees of freedom to uniquely define this, however the equations are not easy so I was kind and made each length in the figure an integer, so that people could chance upon the solution by trying a few integer combinations. The area of the square space is 100.

Solution of the Week #249 - Tetrahedron Packing

It’s tempting to think that the answer is 125, as the space is the volume of 125 unit tetrahedrons, however tetrahedrons cannot pack without leaving gaps.

To the best of my knowledge the most you can fit in is 65:

On the bottom level you can fit 25 pointing upwards and 6 pointing downwards; on the next level up you can fit 16 pointing upwards and 3 pointing downwards; on the middle level you can fit 9 pointing upwards and 1 pointing downwards; on the next level you can fit 4, and a further 1 at the very top, giving a total of 65.

Solution of the Week #248 - Quartet

Call the four numbers we are looking for, in ascending order, a, b, c and d. We know they are strictly ascending because if any were the same, some of the product pairs would be the same too.

ab must be the lowest product 6.

The second lowest product has to be ac = 8.

cd must be the highest product 32.

The second highest product has to be bd = 24.

However for the other two products we have a choice. In the original quartet of 2,3,4 and 8, ad = 16 and bc = 12. If we now assign those products the other way round we should end up with a different quartet of numbers. So:

ab=6

ac=8

ad=12

bc=16

bd=24

cd=32

If we multiply ab by ac and then divide by bc we will have a^2 = 3. Therefore a = sqrt(3) = 1.732

We can easily work out the others now:

b = 6/sqrt(3) = (2)sqrt(3) = 3.464

c = 8/sqrt(3) = (8/3)sqrt(3) = 4.619

d = 12/sqrt(3) = (4)sqrt(3) = 6.928

The sum of this quartet is 16.743, so is indeed less than the 17 total of the original quartet.

Solution of the Week #247 - Diophantine Parallelogram

By alternate angles ADC is also equal to the two equal corners at point A. By isosceles triangle, ABD is also the same angle.

Therefore triangles ADB and ACD are similar. AD:AB = CD:AD.

Let CD = x^2 and AB = y^2. It follows that AD =xy.

We are told y^2 – x^2 = 13, therefore (y+x)(y-x) = 13.

The only integer solutions to this is y=7, x=6, therefore AD = 42.

(Pedantic note: x and y don’t necessarily need to be integers for x^2, xy, y^2 and (y^2)-(x^2) all to be integers, eg sqrt(2) and sqrt(8) would satisfy. Basically either x and y are integers, or y/x is an integer, (or both). However since they represent the sides of a triangle, y/x must be between 1 and 2, so y=7, x=6 is the only solution).

Solution of the Week #246 - Ghost Crossword

Method of solving: Numbers 1, 12 and 15 appear in both lists, so because of rules 1 and 2, they must either be on the top-left-bottom-right diagonal, or in pairs in corresponding position either side of it. Rule 6 means that 1 must be on the top row, so is either in top corner or in corresponding position in top row that 12 is in left-hand column. 1 cannot be in second column, as there are too many numbers for 12 to be in second row. If 1 is in third column or beyond, then either a 2x2 black square appears in the corner, or another number must lie on TLBR diagonal. Neither of these are allowed, so 1 must be in top left corner. 

Now 4 across must also be on the top row to mirror 1 across (as 1 across is not allowed to fill the entire row). 4 must either be in 6th column or 7th column, depending on whether 1 across and 4 across are three or four ‘letters’ long. As 4 is across only, and not down, any attempt to make it three ‘letters’ long leads to a contradiction, therefore it is in the 6th column, and the square immediately to the left and below it are black. When you place a white or a black square, you can use rule 2 to transfer it around the grid, and very quickly the grid takes shape. 

Solution of the Week #245 - Three Digits

ABC = 239.

239 and 293 are prime.

329 = 7 x 47.

923 = 13 x 71.

392 = 2^3 x 7^2. Its proper divisors are: 1, 2, 4, 7, 8, 14, 28, 49, 56, 98 and 196. Their sum is 463, which is 71 greater than 392.

932 = 2^2 x 233. Its proper divisors are: 1, 2, 4, 233 and 466. Their sum is 706, which is 226 less than 932.

Solution of the Week #244 - Three Way Split

The following is simple proof that the 1 2/3 solution can be improved upon:

However, we can do even better using circular arcs, such that any junctions with the edge of the square are at right angles and any junctions within the square are at 120 degrees:

As far as I can ascertain, this is now the shortest overall cut length but if you can do better I would be interested in knowing about it!

Solution of the Week #243 - Shaded Circles

The ring option is fairly easy to calculate: each of the nine circles will have an area of pi/4, therefore the shaded are is 9pi/4 = 7.069…

The crescent area is trickier.

The radius of the largest shaded circle is 1, the next is 2/3, the next 1/3, then 2/11… Naming the largest circle the zeroth, in general the radius of the nth circle is:

2/(n^2 + 2). The area of each circle is pi.r^2 or:

pi*(2/(n^2+2))^2. Usefully this also works for negative values of n, so will cover both arms of the crescent.

At this point I consulted the Wolfram Alpha website to see if the infinite sum of this boils down to anything simple:

sum_(n=-∞)^∞ π (2/(n^2 + 2))^2 = 1/2 π^2 (sqrt(2) coth(sqrt(2) π) + 2 π csch^2(sqrt(2) π))

Either using Wolfram Alpha or Excel we can estimate the infinite sum as ≈ 6.998…

Therefore the ring option gives a slightly larger shaded area.