sqrt(sqrt(80)+sqrt(81))
= sqrt(4*sqrt(5) + 9)
= sqrt(4 + 4*sqrt(5) + 5)
= sqrt(2^2 + 2*2*sqrt(5) + sqrt(5)^2)
= sqrt(2 + sqrt(5))^2
= 2 + sqrt(5)
Solution of the Week #430 - 1x1x1 Rubik's Cube
The perhaps surprising answer is that every scramble can be solved in at most TWO adjacent colour swaps. The way I approached it was to separate the scrambles into three possible cases, based on the number of opposite pairs present in the scramble. This can be 0, 1 or 3. There can’t be exactly two opposite pairs present because if there were, the third opposite pair would also be there!
Of the 30 possible distinct cube arrangements, 16 are of the ‘no opposite pairs’ type, 12 have exactly one opposite pair and 2 have all three opposite pairs.
When there are three opposite pairs, you either already have the solved state or a complete mirror image of the solved state. For the mirror image you can just swap the blue and white, and the green and yellow, for instance, and you have solved the cube.
For the case where there is one opposite pair, let’s assume without loss of generality that the red and orange are opposite, but that green-blue and white-yellow are not. Looking at the RWB vertex, either it is already clockwise, in which case swapping GY will solve the cube, or RWB is anti-clockwise, in which case swapping WB will solve the cube. If Blue and White are opposite, then the RWB vertex won’t exist, but the RBY vertex will, and the same situation arises. So for the 1 opposite pair case, one swap is always enough.
For the case where none of the opposite pairs start off opposite, if you swap any one side so that it IS opposite its partner, for instance by swapping the Orange to the position opposite the Red, and you will reduce to the case where there is exactly one opposite pair present (the RO pair), and as we have already seen, that case can always be solved in just one move.
QED.
Solution of the Week #429 - Strange Stamps
There are three ways to do it:
1, 2, 5, 8, 11, 12, 13
1, 3, 4, 9, 10, 12, 13
1, 3, 5, 7, 8, 17, 18
Solution of the Week #428 - Doubly Generated Hexagon
Solution of the Week #427 - House Numbers part 2
There are 68 houses on the street.
Oddy lives at number 31 and Evelyn lives at number 56.
The odd numbers from 1 to 29 add to 225.
The odd numbers from 33 to 67 add to 900.
The even numbers from 2 to 54 add to 756.
The even numbers from 58 to 68 add to 378.
Solution of the Week #426 - House Numbers
The sum of the first n odd numbers is simply n^2. If I live at the kth house (ie house number 2k-1) then the houses to the left of it add to (k-1)^2. For example if I lived at number 7 (the fourth odd number) 1+3+5 is equal to 3^2 = 9.
For the houses to the right, if there are n houses altogether then we will have n^2 – k^2. This needs to be equal to (k-1)^2.
Effectively then, we are looking for two consecutive square numbers (k-1)^2 and k^2, which sum to another square number n^2.
Solutions exist when k is 1, 4, 21, 120, 697 etc. Only one of these corresponds to a three digit house number. The 120th odd number is 239. Therefore I live at number 239 in a street with houses up to number 337. House numbers either side of me add up to 14161.
Solution of the Week #425 - Trisected
Consider a simplified generalised version of the figure as below, scaling the figure down by a factor of 15 and letting the 33 be an unknown value for the time being.
From the angle bisector theorem, AB/BD = AF/FD. I’ve called the length of BD ‘a’ hence AB = ax.
ABD is a right-angled triangle, so by Pythagoras we have a^2+(ax)^2=(x+1)^2
a^2(x^2+1)=(x+1)^2
a^2=((x+1)^2)/(x^2+1)
We’ll also use the fact that triangle ABD is similar to triangle BDE, since they share the angle at D and they both have a right angle.
h/a=ax/(x+1)
h=xa^2/(x+1)
But we have another expression for a^2 above, so let’s use that:
h=x(x+1)/(x^2+1)
Now, here’s the clever step. We could have gone through the exact same steps from the right-hand side instead, and found a value for h in terms of y, and we would have ended up with the exact same expression. So it’s also true that:
h=y(y+1)/(y^2+1)
Now, returning to the specific puzzle, we’ll keep the DF=1, but now allow x=33/15, so we just have a scaled down version of the real puzzle.
Plugging x=33/15 into the expression gives us h=88/73.
88/73=y(y+1)/(y^2+1)
Cross-multiplying and multiplying out we get the quadratic:
15y^2-73y+88=0
This has the two solutions 33/15 and 40/15. We already knew about 33/15 as that was the value of x that we plugged in. So y=40/15.
Rescaling so that FD is once again equal to 15, we find that the missing value from the puzzle is 40.
There is arithmetically an easier method but it’s harder to see how it’s justified or why it works. And that is that the locus of points that are a constant ratio from C and F respectively is a circle whose diameter is AD. Once you know that, calculating the missing length is relatively straightforward.
?/15 = (?+48)/33
33? = 15? = 720
18? = 720
? = 40.
Solution of the Week #424 - Sock Drawer
The ‘G’ pair of socks are touching.
Solution of the Week #423 - Triangle 29
If the triangle has base 5 and height 2, then it will have hypotenuse of square root of 29. The smaller copies will therefore have hypotenuse of 1 and can fit together as below:
Solution of the Week #422 - Boggle E
Badge, bead, beck, café, code, complied, deaf, deck, face, faced, fade, gecko, head, heck, lied, life, mode.
Solution of the Week #421 - Odd Prime Balance
The lowest solution is achieved when T is 6 and U is 24. To find the values of V to Z, just choose the lowest number for which p, p+6 and p+24 are all prime, then the next lowest without overlapping, etc. So, our V to Z are 5, 7, 17, 37 and 47.
Our A to O will then be:
A = 5
B = 7+6 = 13
C = 17+24 = 41
D = 37
E = 47+6 = 53
F = 5+24 = 29
G = 7
H = 17+6 = 23
I = 37+24 = 61
J = 47
K = 5+6 = 11
L = 7+24 = 31
M = 17
N = 37+6 = 43
O = 47+24 = 71
Giving a total of 489, using 15 of the first 20 prime numbers.
Thanks to Graham Holmes for finding this optimal solution.
Solution of the Week #420 - Fourth Powers and Fourth Fractions
The initial step is to try to find a useful factorisation of the general form (n^4 + 1/4).
We will aim to factorise into two factors as below:
(n^2 +mn +1/2)(n^2 –mn +1/2)
Clearly the first terms in each bracket will combine to give the sought after n^4, and the last in each bracket will give the 1/4 we need. The fact that we have +mn and -mn means that the n^3 terms will cancel, as will the n^1 terms. We must then choose a value of m such that the n^2 terms disappear too.
Just showing the n^2 terms, we have (1/2)n^2 +(1/2)n^2 =(m^2)n^2.
m^2 = 1. So m is +/-1 (but since we have +m in one bracket and -m in the other it makes no difference which we choose).
So (n^4 + 1/4) = (n^2 +n +1/2)(n^2 -n +1/2)
We still need some further manipulation before it becomes useful.
If we take the first bracket and rewrite it as:
(n^2 +n +1/4 +1/4)
Then the first three terms form a perfect square:
((n+(1/2))^2 +1/4)
Doing the same for the second bracket we get
((n-(1/2))^2 +1/4)
To see how this is useful, let’s rewrite some of the terms of the initial question in this new form:
(1^4 +1/4) = ((1.5)^2 +1/4)((0.5)^2 +1/4)
(2^4 +1/4) = ((2.5)^2 +1/4)((1.5)^2 +1/4)
(3^4 +1/4) = ((3.5)^2 +1/4)((2.5)^2 +1/4)
The term ((1.5)^2 +1/4) will appear once in the numerator and once in the denominator, and so will cancel out. This will be true for almost all of the terms in the expression and we will just be left with: ((10.5)^2 +1/4)/((0.5)^2 +1/4)
To aid mental calculation, we can rewrite these two terms in the previous form:
(10^2 +10 +1/2)/(0^2 +0 +1/2)
110.5 *2
And so the solution is precisely 221.
Solution of the Week #419 - Minimum Triangle
It is tempting to think that the triangle would need to be Pythagorean. Certainly for any Pythagorean triangle, the values of a and b would be whole numbers, and c would be a rational number. Suitably scaled up, this too can become a whole number. For instance, if we started with a 3-4-5 triangle, a would be 2 and b would be 3. c would work out to be 2.4. Scaling everything by 5 would give a solution of (10,15,12) with a total of 37. This is not however the minimum solution.
It's a nice little fact that the area of such a triangle is simply a*b. It’s simple enough to prove with a bit of algebra; I’ll leave it to the reader to try it. And if you find a nice geometric proof, let me know as thus far one has eluded me!
That being the case, (a+b)*c/2, the standard way of finding the area, must be equal to a*b. Rearranging, we need to find two numbers a and b such that their product divided by their sum is either a whole number or a half number. The first such pair is 2 and 6, yielding the minimum solution of (2,6,3). The area is 12, which is both 2*6 and (2+6)*3/2. So the answer is 11. The resulting triangle is certainly not Pythagorean, having sides (2*sqrt(7)-2, 2*sqrt(7)+2,8).
Solution of the Week #418 - Fourth Circle
Because three of the circles are tangent at the same point, their centres lie on a straight line. That being the case, if we draw lines connecting all of the circle centres, we can form two triangles which both use the angle ‘x’: the 90,120,70 triangle and the (R+70),120,R triangle.
We can use the law of cosines which states:
Cos(a) = (B^2+C^2-A^2)/(2BC), (where side A is opposite angle a)
If we do so first for the 90,120,70 triangle, we find that cos(x) = 22/27.
Now if we do the same for the large triangle, we already know cos(x), so:
22/27 = (140R + 19300)/(240R + 16800)
22(240R + 16800) = 27(140R + 19300)
1500R = 151500
R = 101
So therefore the radius of the fourth circle is 101.
Solution of the Week #417 - Triple Duality
ERA, ATTEND, BISHOP, DEW, TOLERABLE, END, BLEMISHES, BISMILLAH, MILDEW, ADVICE, MISFIT, ARC, ADVERB, HOP, ATTACK, AYATOLLAH, PAPERBACK, FIT, PAPAYA, ARCHES, ICE.
Solution of the Week #416 - 2023 Rectangle Ratio
The first thing to notice is that the area given for the square is not a square number. Since ultimately we are only interested in the ratio of sides of the rectangle, we should have no problem scaling up the figure so that it is. Since 3375 = 3^3 * 5^3, if we multiply this (and the rectangle area) by 15, we will get a square number. The side of the square will then be 225, and the new rectangle area will be 2023*15 = 30345.
The other dimensions in the figure below are related to one another by Pythagoras and similar triangles.
120 + 105 = 225
255 * 119 = 30345
225^2 + 120^2 = 255^2
255/225 = 119/105
Since all those are satisfied, these must be the correct dimensions. Therefore the ratio of the rectangle’s sides is 255/119, which is 15/7.
Solution of the Week #415 - Alchemy
There are probably several solutions, but the one I found is:
CARBON – ACORNS – REASON – ARISEN – SERIAL - SILVER
Solution of the Week #414 - Mystery Sequence
Each number is the lowest number that hasn’t yet appeared in the sequence, that begins with the last letter of the previous number.
ONE – EIGHT – TWO – ONE HUNDRED – DECILLION – NINE – ELEVEN – NINETEEN - NINETY
No numbers begin with ‘y’.
I realise I’ve been a little inconsistent with names of numbers, allowing 100 to be called ‘one hundred’ but 10^33 as merely ‘decillion’ not ‘one decillion’ but that was the only way!
Solution of the Week #413 - Interior Point
Since the lines meet the edges of the square at the midpoints, we can divide the square into pairs of triangles with identical areas as below.
From the puzzle a+b=33, c+d=39, therefore the entire square, 2(a+b+c+d)=144, so the square is 12x12 and the base length of each of the eight triangles is 6. Because it is a square we also know that the a and c triangles make up half the area, and the b and d triangles make up the other. So a+c=b+d=36.
With all of this information we can determine the values of the individual areas to be a=12, b=21, c=24, d=15.
Looking only at the areas a and d will pinpoint the coordinates of the interior point (4,5).
Solution of the Week #412 - Quad in a Quarter
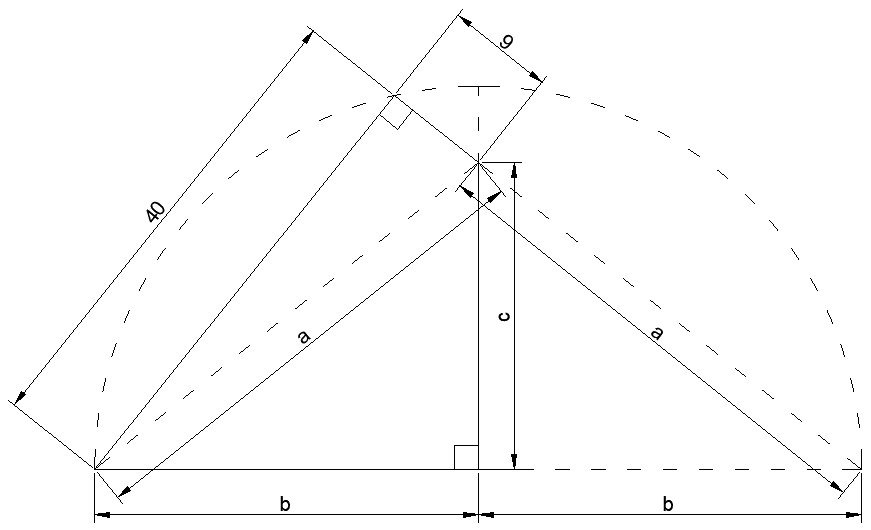
From Pythagoras on the (40,9,a) triangle, the length of a is 41. If we reflect this in the vertical axis we get a line that is collinear to the line of length 9. This gives another right-angled triangle (40,9+a,2b) and using Pythagoras again we find b=5*sqrt(41). Using Pythagoras yet a third time on the (b,c,a) triangle, we find c=4*sqrt(41). Finally to find the area of the quadrilateral we calculate ((40*9)+(b*c))/2, which neatly cancels out the square roots and gives the answer of 590.
Alternatively, the following shortcut means you don’t even have to calculate b or c: notice that the quadrilateral exceeds the 40*9 triangle by the exact same amount that the 40*50 triangle exceeds the quadrilateral. So the quadrilateral will be the average of the areas of the 40*9 triangle and the 40*50 triangle, so (180+1000)/2 = 590.